Designing for Change in Elastic Machine Learning
As everyone working on software knows, the only thing constant is change. When trying to identify anomalies in time series data, one of the major factors that needs to be addressed is how to design the baseline model to effectively respond to changes as new data enters the system. To discover anomalies in dynamic data, we are constantly working on methods that will make Elastic machine learning more effective.
Fundamentally, the systems that we are monitoring are not static. As new users, new features, new pages are added to an application, the baseline model will change. Sometimes these changes are gradual and other times they can be sudden. We want to continually provide the best modeling and are always looking for better techniques for handling multiple types of change in the systems we are monitoring.
Starting with version 6.4 of the Elastic Stack, we have added a significant improvement in the way our machine learning modelling adapts to changes in system behaviour. Before discussing the details of the enhancements we’ve made, it is useful to review modelling in the context of changing systems in general and how we have historically approached this problem. If you want to skip straight to what’s new in 6.4 skip ahead to the ‘What’s new” section.
Types of Change
In a more general setting, such changes are referred to as concept drift: what was true for a (data set, model) pair historically ceases to be true over time. This is a reasonably well studied problem in machine learning because it is critically important to deal with if one wants to use a model indefinitely. If you don’t handle it, a model which was very accurate initially can start to exhibit significant biases over time and become effectively useless. In working on this problem, people typically classify the types of change a system can undergo as recurring changes, gradual changes or sudden changes (or shocks). These are mostly self explanatory, but it is useful to think about them in terms of some concrete examples for time series data.
A recurring change is one which happens repeatedly over a long time span. For example, memory used by a long running process can be subject to recurring drops due to garbage collection. These are usually not completely predictable ahead of time and so should be distinguished from something that is, like seasonal behaviour. The reason for this uncertainty is that the trigger for garbage collection would be the actual memory used by the process. This is subject to a random forcing function, namely, the operations the process performs which will depend on how an external system interacts with it. Equally, these are not unique events: when they occur, they have similar characteristics and depend in predictable ways on the current state of the process.
Gradual changes correspond to a slow drift in the process which generates the time series values. Let’s imagine the total traffic to a website over time. This will have common periodic patterns, which amount to the traffic changing as a function of hour of day or day of week. However, you would expect over time the popularity of the website to increase (or decrease). This could correspond to the traffic being modulated (or multiplied) by some time varying value. For example, the traffic might increase by between 5% and 15% month-on-month and do so subject to some stable (probability) distribution. An important property of such systems is they typically change smoothly. This means the increase in the traffic one observed last week, as compared to a month ago, will be a better predictor for the increase in the week to come.
Finally, sudden changes correspond to an unpredictable and discontinuous change in the process generating the time series values. By way of an example, consider the rate of data indexed into an Elasticsearch cluster. If one is ingesting application log files this will be some smooth function of time. However, when someone adds a new data source the rate will change in a discontinuous fashion at this time. In particular, it will experience a step increase whose magnitude is equal to the rate of data from this new source.
Modelling the Types of Change
How one deals with different types of change from a modelling standpoint is quite dependent on the type of model one is using. It is also important to realise that different types of change are best dealt with in different ways, and this is independent of the choice of model. In practice, people do not always adopt the best approach for their data characteristics because other constraints make this difficult. For example, a simple, widely used approach is to periodically retrain on a sliding time window of historical data. This is attractive because it is easy to apply to any model. However, for a gradually changing system it has some significant disadvantages. It makes poor use of computational resource, typically processing the same piece of data many times during the train step and can lead to instabilities when the model is retrained.
Instead, the basic modelling techniques we use are all online. We incorporate each new piece of data into our model and then discard that piece of data, and such formulations naturally pick up ways to allow the model parameters to change smoothly over time. We also have a natural way of learning the rate at which to do this from the data. In particular, we use a simple feedback controller to adjust the rate of change of the model parameters as a function of the error in the distribution we predict for the next value we’ll see. This fits our use case well since we first detect a change in the system, flag an anomaly, but then adapt to it at an accelerated rate.
A useful way of thinking about this approach is that our models are continuously learning a horizon of relevant historical data given the predictive power of the model with respect to the data set at hand. This horizon is a function of the ability of the model to capture recent behaviour of the time series. One finds that a more expressive model, or more precisely, a model which is better able to capture the particular behaviour of the time series, is able to use more historic data without suffering from significant error in the distribution it predicts for the next value.
In this context, it is important to strike a balance between how quickly the model is able to change and whether it fits anomalous behaviour. Ideally, anomalous time intervals should be entirely ignored by the model. But there is a problem, because one doesn’t know in advance how the future will play out and whether the values constitute an anomaly or some permanent system change. For our model, which continually learns, this amounts to how quickly it adapts its parameters to new behaviour. Aside from the rate at which we allow the model parameters to change, we automatically back off how much it learns from new values based on how unlikely they are given its current expectations. The more unlikely the values, the less notice the model takes of them. Formally, this provides a continuous parameterisation of classes of robust estimating functions for the components of our model. It is worth noting that this also means that the more history our model is able to use, the more confident it can be that values are unusual and so the less notice it’ll take of anomalous intervals.
To summarise, for gradually changing systems, our modelling prior to 6.4 performed well, was stable and computationally efficient. However, starting with version 6.4, we wanted to improve our behaviour with respect to sudden changes, and to do this whilst maintaining or even improving our handling of gradual change.
What’s New in 6.4
In Elastic Stack 6.4, we introduced a change which assumes parametric forms for sudden changes to time series. As a result, we are able to use standard model selection techniques to decide if the system has undergone one of these changes. This approach is complementary to our existing approach to adapt to gradual changes; it simply functions side-by-side with it. Importantly, in systems which undergo sudden changes, it means we can use more history whilst avoiding errors in our predicted distribution. It, therefore, has an incidental advantage that, for these systems, our models are more robust to anomalous intervals, because they remember more history and so take less notice of them.
It might seem that assuming simple parametric descriptions for types of change is overly restrictive, but it has some big practical advantages. There is good reason to have inductive bias in this process, because, in practice, one often sees similar types of sudden changes. For example, periodic data undergoes some linear scaling, an otherwise continuous time series undergoes a step change and a periodic pattern experiences a shift in time.
To understand how linear scaling can commonly arise, consider any system which uses load balancing and experiences a constant external seasonal forcing function, such as traffic to a website. It will exhibit linear scaling for individual metrics during failover or if compute resources are added or removed. Level shifts often occur in otherwise smooth metrics at any point when resources are added or recovered, such as when a file is copied or garbage collection occurs. This is because these processes typically act over a relatively short time scale.
Having simple parametric descriptions of possible changes means we can identify changes and learn the new model parameters quickly, both of which are important to minimize the “down time” for anomaly detection, i.e. when prediction error is high. Finally, we can detect these classes of change with high accuracy, which is important to avoid fitting anomalous data.
Sudden Change Example
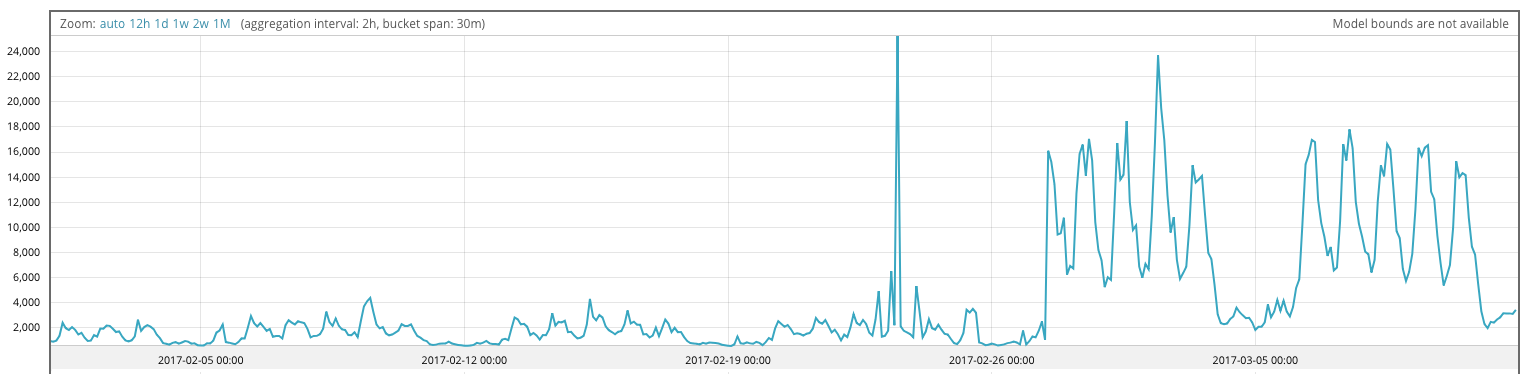
We’ll finish up by reviewing a couple of examples of the way the model adapts to sudden changes as a result of the enhancements in version 6.4. The first example is a prototypical linear scaling. This data set comprises the total count of 404 statuses generated by visitors to a website. A code change resulted in a sudden increase in the number of 404s around 28th February 2017. We expect a linear scaling to occur at this point because the chance of a 404 increased while the seasonal traffic to the website remained more or less unchanged.
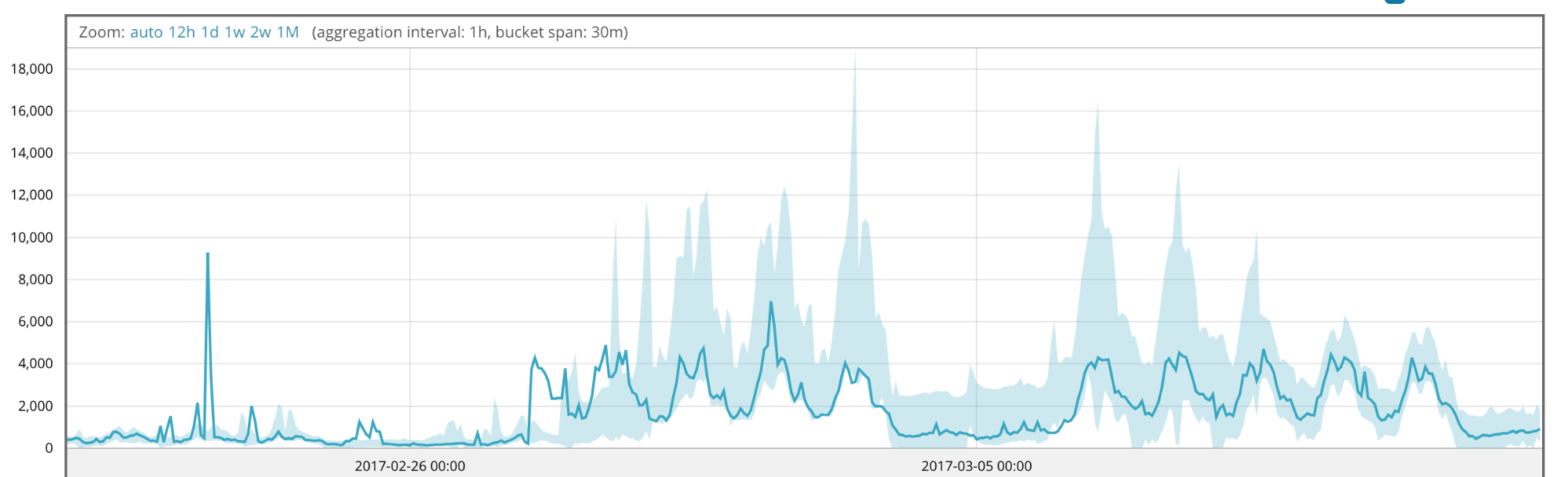
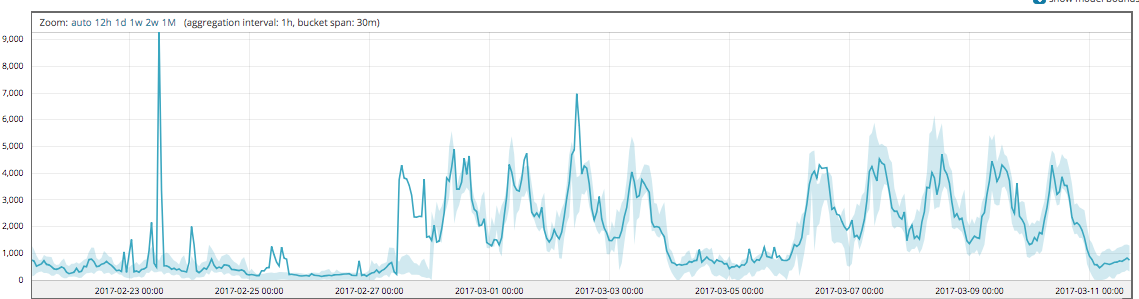
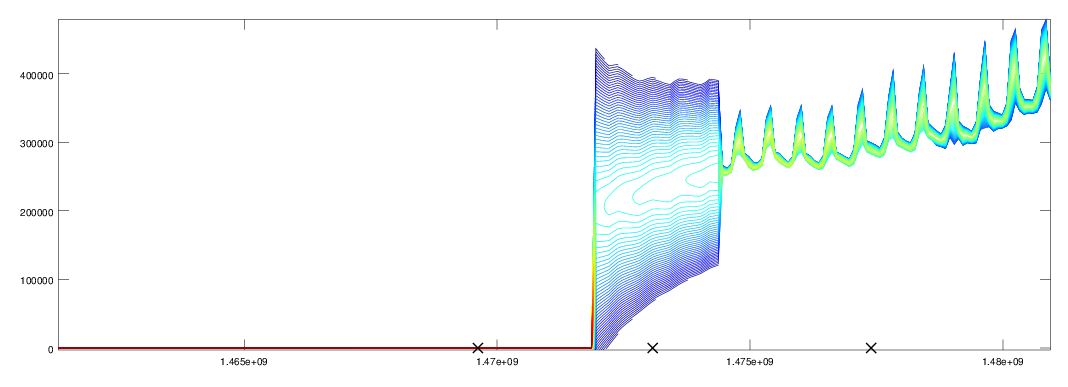
Figures 1, 2 and 3 show the model bounds which can be viewed in the Single Metric Viewer tab. Figure 1 shows the traffic pattern and Figures 2 and 3 highlight the difference in our modeling technique before and after version 6.4. It should be clear from the second two figures that we largely ignore the values associated with the scaling initially. This is because, as discussed above, we reweight highly unusual values when updating the model.
You will notice the benefits of of 6.4 modeling enhancements In Figure 3, just before midnight on the 28th February, we create a new mode for the values we’ve seen for the preceding 6 hours. Around 6 hours later, we detect the scaling event and start using the scaled model. Note that because we maintain a copy of the prediction error distribution updated conditionally on there having been a scaling event, the distribution narrows significantly at this point.
Seasonality and Step Change Example
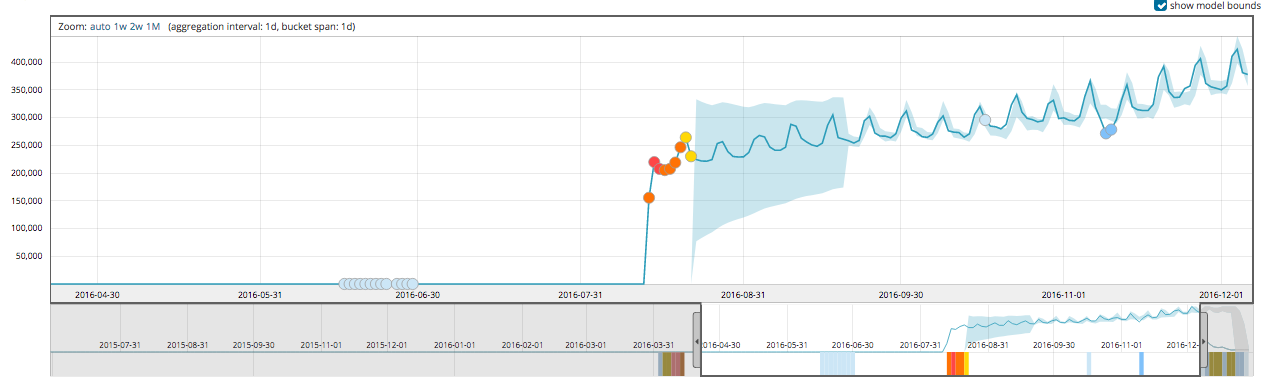
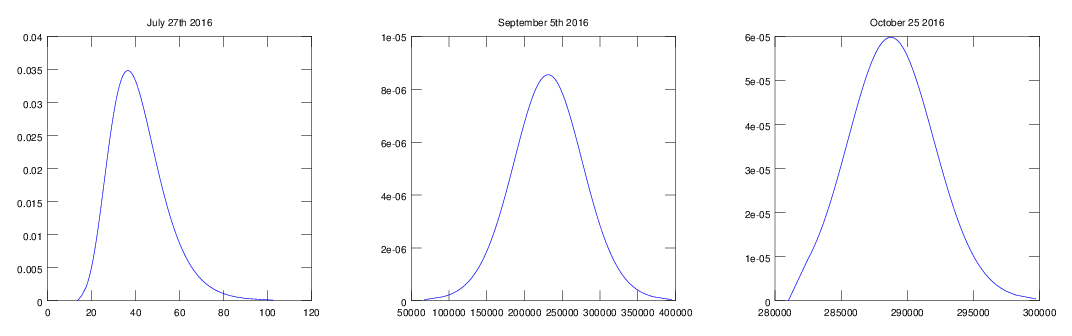
The next example shows the model adapting to a step discontinuity in the values. In fact, this is complicated by the fact that the data also becomes seasonal, with weekly period, after the change point. Figures 4, 5 and 6 show the model bounds, log of the predictive distribution and snapshots of the predictive distribution for daily hits on a webpage page. It is visually very clear that around 14th August 2016 something changes significantly in this process. The model learns the new level and trend fairly quickly. It then takes around 5 repeats to learn the new seasonality and reassess the prediction error distribution in this context. At this point it is able to predict the values accurately and so it picks up the unusually low values, given the new behaviour, at the beginning of November.
Summary
As you can see there is a lot of work that happens behind the scenes to make Elastic machine learning modeling more effective at identifying anomalies. With time series data, the model needs to be continually updated to respond to dynamic data. Starting in 6.4, we have improved the way our modeling adapts to changes in system behaviour to make sure that you get better results.
Try it out for yourself on your data, download the Elastic Stack and enable the 30-day trial license, or start a free trial on Elastic Cloud.