O que é kNN?
Definição de k vizinhos mais próximos
O kNN, ou algoritmo dos k vizinhos mais próximos, é um algoritmo de machine learning que usa proximidade para comparar um ponto de dados com um conjunto de dados no qual ele foi treinado e memorizado para fazer previsões. Esse aprendizado baseado em instância confere ao kNN a denominação de “aprendizado preguiçoso” e permite que o algoritmo execute problemas de classificação ou regressão. O KnN parte do pressuposto de que pontos semelhantes podem ser encontrados próximos uns dos outros — aves da mesma espécie voam juntos.
Como algoritmo de classificação, o kNN atribui um novo ponto de dados ao conjunto majoritário dentro de seus vizinhos. Como algoritmo de regressão, o kNN faz uma previsão com base na média dos valores mais próximos do ponto de consulta.
O kNN é um algoritmo de aprendizado supervisionado no qual o “k” representa o número de vizinhos mais próximos considerados no problema de classificação ou regressão, e “NN” representa os vizinhos mais próximos do número escolhido para k.
Breve história do algoritmo kNN
O kNN foi desenvolvido por Evelyn Fix e Joseph Hodges em 1951 no contexto de uma pesquisa realizada para os militares dos EUA1. Eles publicaram um artigo explicando a análise discriminante, que é um método de classificação não paramétrica. Em 1967, Thomas Cover e Peter Hart expandiram o método de classificação não paramétrica e publicaram seu artigo “Nearest Neighbor Pattern Classification” (Classificação de padrões de vizinhos mais próximos)2. Quase 20 anos depois, o algoritmo foi refinado por James Keller, que desenvolveu um “kNN difuso” que produz taxas de erro mais baixas3.
Hoje, o algoritmo kNN é o algoritmo mais utilizado devido à sua adaptabilidade à maioria das áreas — desde genética até finanças e atendimento ao cliente.
Como funciona o kNN?
O algoritmo kNN funciona como um algoritmo de aprendizagem supervisionado, o que significa que é alimentado com conjuntos de dados de treinamento que memoriza. Ele se baseia nesses dados de entrada rotulados para aprender uma função que produz uma saída apropriada quando recebe novos dados não rotulados.
Isso permite que o algoritmo resolva problemas de classificação ou regressão. Embora a computação do kNN ocorra durante uma consulta e não durante uma fase de treinamento, ele tem requisitos importantes de armazenamento de dados e, portanto, depende fortemente da memória.
Para problemas de classificação, o algoritmo KNN atribui um rótulo de classe com base na maioria, o que significa que usará o rótulo que estiver presente com mais frequência em torno de um determinado ponto de dados. Em outras palavras, a saída de um problema de classificação é o modo dos vizinhos mais próximos.
Uma distinção: votação por maioria X votação por pluralidade
A votação por maioria denota qualquer coisa acima de 50% como maioria. Isso se aplica se há dois rótulos de classe em consideração. No entanto, a votação por pluralidade se aplica se vários rótulos de classe estão sendo considerados. Nesses casos, qualquer valor superior a 33,3% seria suficiente para denotar uma maioria e, portanto, fornecer uma previsão. A votação por pluralidade é, portanto, o termo mais preciso para definir o modo do kNN.
Se fôssemos ilustrar essa distinção:
Uma previsão binária
Y: 🎉🎉🎉❤️❤️❤️❤️❤️
Voto por maioria: ❤️
Voto por pluralidade: ❤️
Um ambiente multiclasse
Y: ⏰⏰⏰💰💰💰🏠🏠🏠🏠
Voto por maioria: Nenhum
Votação plural: 🏠
Os problemas de regressão usam a **média** dos vizinhos mais próximos para prever uma classificação. Um problema de regressão produzirá números reais como saída da consulta.
Por exemplo, se você estivesse criando um gráfico para prever o peso de alguém com base na altura, os valores que indicam a altura seriam independentes, enquanto os valores do peso seriam dependentes. Ao realizar um cálculo da relação média entre altura e peso, você pode estimar o peso de alguém (a variável dependente) com base na sua altura (a variável independente).
Quatro tipos de cálculo de métricas de distância kNN
A chave para o algoritmo kNN é determinar a distância entre o ponto de consulta e os outros pontos de dados. A determinação das métricas de distância permite o estabelecimento de limites de decisão. Esses limites criam diferentes regiões de pontos de dados. Existem diferentes métodos usados para calcular a distância:
- A distância euclidiana é a medida de distância mais comum, que mede uma linha reta entre o ponto de consulta e o outro ponto que está sendo medido.
- A distância de Manhattan também é uma medida de distância popular, que mede o valor absoluto entre dois pontos. É representada em uma grade e muitas vezes chamada de geometria do táxi — como você viaja do ponto A (seu ponto de consulta) ao ponto B (o ponto que está sendo medido)?
- A distância de Minkowski é uma generalização das métricas de distância euclidiana e de Manhattan, que permite a criação de outras métricas de distância. É calculada em um espaço vetorial normatizado. Na distância de Minkowski, p é o parâmetro que define o tipo de distância utilizado no cálculo. Se p=1, então a distância de Manhattan é usada. Se p=2, então a distância euclidiana é usada.
- A distância de Hamming, também conhecida como métrica de sobreposição, é uma técnica usada com vetores booleanos ou de string para identificar onde os vetores não correspondem. Em outras palavras, mede a distância entre duas strings de igual comprimento. É especialmente útil para códigos de detecção e correção de erros.
Como escolher o melhor valor de k
Para escolher o melhor valor de k — o número de vizinhos mais próximos considerados —, você deve experimentar alguns valores para encontrar o valor de k que gera as previsões mais precisas com o menor número de erros. A determinação do melhor valor é um ato de equilíbrio:
- Valores de k baixos tornam as previsões instáveis.
Veja este exemplo: um ponto de consulta é cercado por 2 pontos verdes e um triângulo vermelho. Se k=1 e acontecer que o ponto mais próximo do ponto de consulta seja um dos pontos verdes, o algoritmo preverá incorretamente um ponto verde como resultado da consulta. Valores baixos de k são de alta variância (o modelo se ajusta muito aos dados de treinamento), alta complexidade e baixo viés (o modelo é complexo o suficiente para se ajustar bem aos dados de treinamento). - Valores de k altos têm muito ruído.
Um valor de k mais alto aumentará a acurácia das previsões porque há mais números para calcular os modos ou médias. No entanto, se o valor de k for muito alto, provavelmente resultará em baixa variância, baixa complexidade e alto viés (o modelo NÃO é complexo o suficiente para ajustar bem os dados de treinamento).
Idealmente, você deseja encontrar um valor de k que esteja entre alta variância e alto viés. Recomenda-se também escolher um número ímpar para k para evitar empates na análise de classificação.
O valor de k correto também é relativo ao seu conjunto de dados. Para escolher esse valor, você pode tentar encontrar a raiz quadrada de N, onde N é o número de pontos de dados no conjunto de dados de treinamento. As táticas de validação cruzada também podem ajudar a escolher o valor de k mais adequado ao seu conjunto de dados.
Vantagens do algoritmo kNN
O algoritmo kNN é frequentemente descrito como o algoritmo de aprendizagem supervisionada “mais simples”, o que leva a suas diversas vantagens:
- Simples: kNN é fácil de implementar devido à sua simplicidade e acurácia. Como tal, é frequentemente um dos primeiros classificadores que um cientista de dados aprenderá.
- Adaptável: assim que novas amostras de treinamento são adicionadas ao seu conjunto de dados, o algoritmo kNN ajusta suas previsões para incluir os novos dados de treinamento.
- Facilmente programável: o kNN requer apenas alguns hiperparâmetros — um valor de k e uma métrica de distância. Isso o torna um algoritmo razoavelmente descomplicado.
Além disso, o algoritmo kNN não requer tempo de treinamento porque armazena dados de treinamento e seu poder computacional é usado apenas ao fazer previsões.
Desafios e limitações do kNN
Embora o algoritmo kNN seja simples, também apresenta alguns desafios e limitações, em parte devido à sua simplicidade:
- Difícil de dimensionar: como o kNN ocupa muita memória e armazenamento de dados, aumenta as despesas associadas ao armazenamento. Essa dependência da memória também significa que o algoritmo é computacionalmente intensivo, o que, por sua vez, consome muitos recursos.
- Maldição da dimensionalidade: refere-se a um fenômeno que ocorre na ciência da computação, em que um conjunto fixo de exemplos de treinamento é desafiado por um número crescente de dimensões e pelo aumento inerente de valores de recursos nessas dimensões. Em outras palavras, os dados de treinamento do modelo não conseguem acompanhar a dimensionalidade em evolução do hiperespaço. Isso significa que as previsões se tornam menos precisas porque a distância entre o ponto de consulta e pontos semelhantes aumenta — em outras dimensões.
- Sobreajuste: o valor de k, como mostrado anteriormente, terá impacto no comportamento do algoritmo. Isso pode acontecer especialmente quando o valor de k é muito baixo. Valores mais baixos de k podem superajustar os dados, enquanto valores mais altos de k “suavizarão” os valores de previsão porque o algoritmo calcula a média dos valores em uma área maior.
Principais casos de uso de kNN
O algoritmo kNN, popular por sua simplicidade e acurácia, apresenta uma variedade de aplicações, especialmente quando usado para análise de classificação.
- Classificação de relevância: o kNN usa algoritmos de processamento de linguagem natural (PLN) para determinar quais resultados são mais relevantes para uma consulta.
- Pesquisa de similaridade para imagens ou vídeos: a busca por similaridade de imagens usa descrições em linguagem natural para encontrar imagens correspondentes a consultas de texto.
- Reconhecimento de padrões: o kNN pode ser usado para identificar padrões em texto ou classificação de dígitos.
- Finanças: no setor financeiro, o kNN pode ser usado para previsões do mercado de ações, taxas de câmbio etc.
- Recomendações de produtos e mecanismos de recomendação: pense na Netflix! “Se você gostou disso, achamos que também vai gostar de...” Qualquer site que use uma versão dessa frase, abertamente ou não, provavelmente está usando um algoritmo kNN para alimentar seu mecanismo de recomendação.
- Saúde: no campo da medicina e da pesquisa médica, o algoritmo kNN pode ser usado em genética para calcular a probabilidade de certas expressões genéticas. Isso permite que os médicos prevejam a probabilidade de câncer, ataques cardíacos ou outras condições hereditárias.
- Pré-processamento de dados: o algoritmo kNN pode ser usado para estimar valores ausentes em conjuntos de dados.
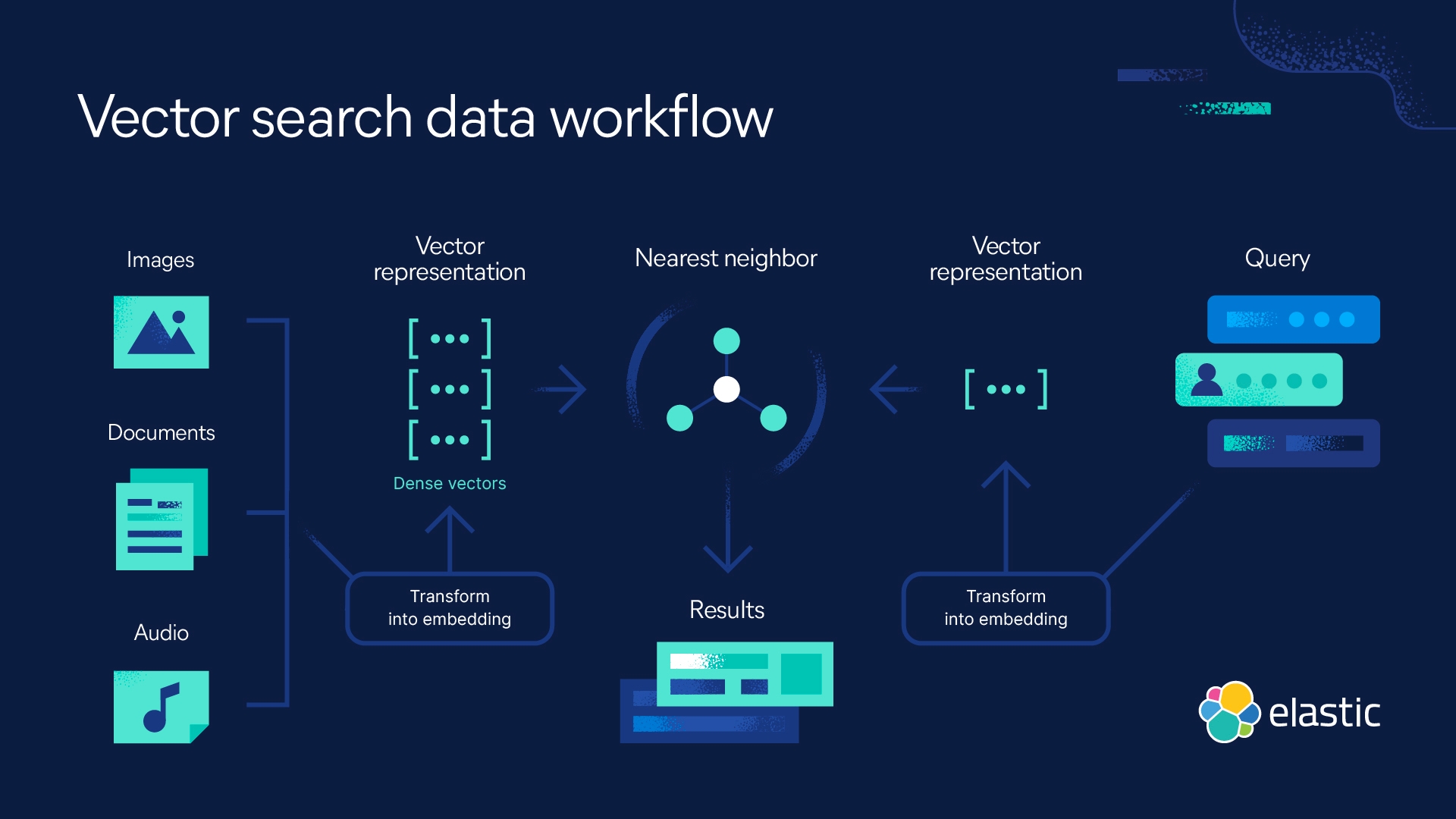
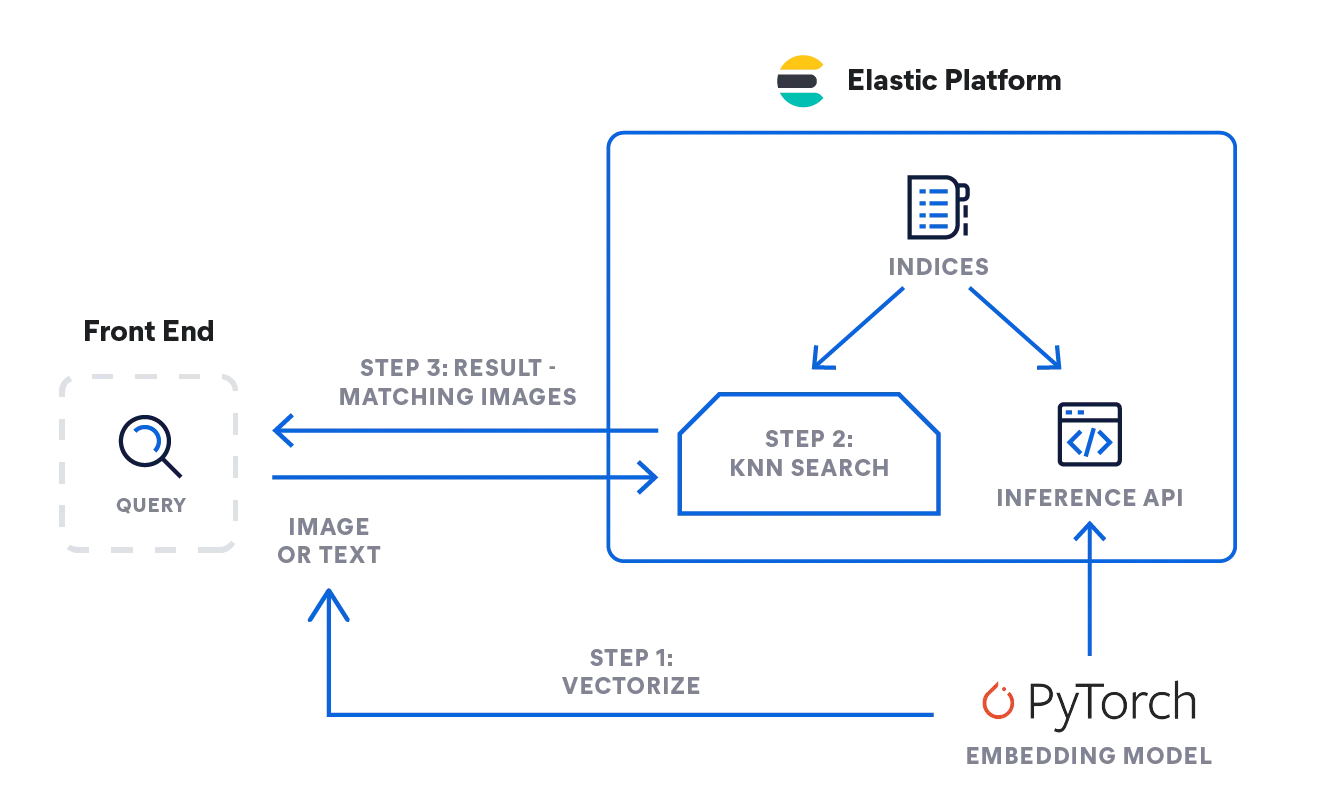
Elastic e a busca com kNN
O Elasticsearch permite implementar a busca com kNN. Dois métodos são aceitos: kNN aproximado e kNN exato de força bruta. Você pode usar a busca com kNN no contexto de busca por similaridade, classificação de relevância baseada em algoritmos de PLN e recomendações de produtos e mecanismos de recomendação.
Perguntas frequentes sobre k vizinhos mais próximos
Quando usar kNN?
Use o kNN para fazer previsões com base na similaridade. Como tal, você pode usar o kNN para classificação de relevância no contexto de algoritmos de processamento de linguagem natural, para mecanismos de recomendação e busca por similaridade ou recomendações de produtos. Observe que o kNN é útil quando você tem um conjunto de dados relativamente pequeno.
O kNN é machine learning supervisionado ou não supervisionado?
O kNN é machine learning supervisionado. Ele é alimentado com um conjunto de dados que armazena e só processa os dados quando consultado.
O que significa kNN?
kNN significa algoritmo de k vizinhos mais próximos, onde k denota o número de vizinhos mais próximos considerados na análise.
Notas de rodapé
- Silverman, B.W., & Jones, M.C. (1989). E. Fix and J.L Hodes (1951): An Important Contribution to Nonparametric Discriminant Analysis and Density Estimation: Commentary on Fix and Hodges (1951). International Statistical Institute (ISI) / Revue Internationale de Statistique,57(3), 233–238. https://doi.org/10.2307/1403796
- T. Cover and P. Hart, "Nearest neighbor pattern classification," in IEEE Transactions on Information Theory, vol. 13, no. 1, pp. 21-27, January 1967, doi: 10.1109/TIT.1967.1053964. https://ieeexplore.ieee.org/document/1053964/authors#authors
- K-Nearest Neighbors Algorithm: Classification and Regression Star, History of Data Science, Accessed: 10/23/2023, https://www.historyofdatascience.com/k-nearest-neighbors-algorithm-classification-and-regression-star/