Accelerating vector search with SIMD instructions
.jpg)
For many years now, code running on the Java Platform has benefited from automatic vectorization — superword optimizations in the HotSpot C2 compiler that pack multiple scalar operations into a SIMD (Single Instruction Multiple Data) vector instruction. This is great, but these kinds of optimizations are somewhat brittle, have natural complexity limits, and are constrained by the Java Platform specification (e.g., strict ordering of floating point arithmetic). This is not to say that such optimizations are not still valuable, just that there are cases where being explicit about the shape of the code can have significantly better performance. The low-level primitive operations supporting vector search in Lucene is one such case.
This article takes a look at the low-level primitives used in Lucene's vector search, how they reliably compile at runtime to SIMD instructions, such as AVX instructions on x64 and NEON instructions on AArch64, and finally what impact this has on performance.
Low-level primitives
At the heart of Lucene's vector search implementation lie three low-level primitives used when finding the similarity between two vectors: dot product, square, and cosine distance. There are floating point and binary variants of each of these operations. For the sake of brevity, we'll look at just one of these primitive operations — dot product. The interface is trivial and looks like this:
/** Calculates the dot product of the given float arrays. */
float dotProduct(float[] a, float[] b);Until now, these primitive operations have been backed by scalar implementations, with consideration given to performance by using existing known techniques, like hand unrolled loops. This is about as good as it gets if you're writing Java code — the rest we leave to the HotSpot Just-In-Time compiler to do the best it can (e.g., auto-vectorization).Here's a simplified scalar implementation of dot product, with unrolling removed (the real implementation can be seen here):
public float dotProduct(float[] a, float[] b) {
float res = 0f;
for (int i = 0; i < a.length; i++) {
res += a[i] * b[i];
}
return res;
}What's changed recently is that the JDK now offers an API for expressing computations that can be reliably compiled at runtime to SIMD instructions. This is OpenJDK's Project Panama Vector API. Of course, the actual instructions that are generated at runtime are subject to what the underlying platform supports (e.g., AVX2 or AVX 512), but the API is structured to cater for this. Again, here is a simplified version of the dot product code, but this time using the Panama Vector API:
static final VectorSpecies<Float> SPECIES = FloatVector.SPECIES_PREFERRED;
public float dotProductNew(float[] a, float[] b) {
int i = 0;
float res = 0f;
FloatVector acc = FloatVector.zero(SPECIES);
int upperBound = SPECIES.loopBound(a.length);
for (; i < upperBound; i += SPECIES.length()) {
FloatVector va = FloatVector.fromArray(SPECIES, a, i);
FloatVector vb = FloatVector.fromArray(SPECIES, b, i);
acc = acc.add(va.mul(vb));
}
// reduce
res = acc.reduceLanes(VectorOperators.ADD);
// tail
for (; i < a.length; i++) {
res += b[i] * a[i];
}
return res;
}You can see that the code is a little more verbose, but it's idiomatic and quite straightforward to reason about how it maps to the hardware at runtime, since you can see the vector operations right there in the code. The VectorSpecies contains the element type, float in our case, and shape, the bit-size of the vector. The preferred species is one of maximal bit-size for the platform. First, there is a loop that iterates over the inputs, multiplying and accumulating SPECIES::length elements at a time. Second, reduce the accumulator vector. And finally, a scalar loop that deals with any remaining "tail" elements.
When we run this code on a CPU that supports AVX 512, we see that the HotSpot C2 compiler emits AVX 512 instructions. Advanced Vector Extensions (AVX) are widely available, with like say CPUs based on Intel's Ice Lake microarchitecture and cloud compute instances based on such (e.g., GCP or AWS). The AVX 512 instructions stride over the dot product computation 16 values at a time; 512 bit-size / 32 bits-per-value = 16 values per loop iteration. When run on a CPU that supports AVX2, one loop iteration of the same code strides over 8 values per iteration. Similarly, NEON (128 bit) will stride over 4 values per loop iteration.
To see this, we need to look at the generated code. Let the fun begin!
Going native
The following is the disassembly of the HotSpot C2 compiler for dotProduct, when run on my Rocket Lake that supports AVX 512.
The snippet below contains the main loop body, where the rcx and rdx registers hold an address pointing to the first and second float arrays.
- First, we see a vmovdqu32 instruction that loads 512 bits of packed doubleword values from a memory location into the zmm0 register — that's 16 values from an offset into the first float[].
- Second, we see a vmulps instruction that multiplies the packed single precision floating-point values previously loaded into zmm0 with the corresponding packed doubleword values from a memory location — that's 16 values from an offset into the second float[], and stores the resulting floating-point values in zmm0.
- Third, we see vaddps that adds 16 packed single precision floating-point values from zmm0 with zmm4 , and stores the packed single precision floating-point result in zmm4 - zmm4 is our loop accumulator.
- Finally, there is a small computation that increments and checks the loop counter.
↗ 0x00007f6b3c7243a4: vmovdqu32 zmm0,ZMMWORD PTR [rcx+r10*4+0x10];*invokestatic load {reexecute=0 rethrow=0 return_oop=0}
│ ; - jdk.incubator.vector.FloatVector::fromArray0Template@32
│ ; - jdk.incubator.vector.Float512Vector::fromArray0@3
│ ; - jdk.incubator.vector.FloatVector::fromArray@24
│ ; - org.apache.lucene.util.VectorUtilPanamaProvider::dotProduct@46
│ 0x00007f6b3c7243af: vmulps zmm0,zmm0,ZMMWORD PTR [rdx+r10*4+0x10];*invokestatic reductionCoerced {reexecute=0 rethrow=0 return_oop=0}
│ ; - jdk.incubator.vector.FloatVector::reduceLanesTemplate@78
│ ; - jdk.incubator.vector.Float512Vector::reduceLanes@2
│ ; - org.apache.lucene.util.VectorUtilPanamaProvider::dotProduct@84
│ 0x00007f6b3c7243ba: vaddps zmm4,zmm4,zmm0 ;*invokestatic binaryOp {reexecute=0 rethrow=0 return_oop=0}
│ ; - jdk.incubator.vector.FloatVector::lanewiseTemplate@96
│ ; - jdk.incubator.vector.Float512Vector::lanewise@3
│ ; - jdk.incubator.vector.FloatVector::add@5
│ ; - org.apache.lucene.util.VectorUtilPanamaProvider::dotProduct@84
│ 0x00007f6b3c7243c0: add r10d,0x10
│ 0x00007f6b3c7243c4: cmp r10d,eax
╰ 0x00007f6b3c7243c7: jl 0x00007f6b3c7243a4Don't worry too much about the exact details of the disassembly — they are provided to give more of a sense of what's happening "under the hood," rather than being critical to the understanding. In fact, the above is somewhat simplified since what actually happens is that C2 unrolls the loop, striding over 4 iterations at a time.
0x00007f74a86fa0f0: vmovdqu32 zmm0,ZMMWORD PTR [rcx+r8*4+0xd0]
0x00007f74a86fa0fb: vmulps zmm0,zmm0,ZMMWORD PTR [rdx+r8*4+0xd0]
0x00007f74a86fa106: vmovdqu32 zmm2,ZMMWORD PTR [rcx+r8*4+0x90]
0x00007f74a86fa111: vmulps zmm2,zmm2,ZMMWORD PTR [rdx+r8*4+0x90]
0x00007f74a86fa11c: vmovdqu32 zmm3,ZMMWORD PTR [rcx+r8*4+0x10]
0x00007f74a86fa127: vmulps zmm3,zmm3,ZMMWORD PTR [rdx+r8*4+0x10]
0x00007f74a86fa132: vmovdqu32 zmm4,ZMMWORD PTR [rcx+r8*4+0x50]
0x00007f74a86fa13d: vmulps zmm4,zmm4,ZMMWORD PTR [rdx+r8*4+0x50]
0x00007f74a86fa148: vaddps zmm1,zmm1,zmm3
0x00007f74a86fa14e: vaddps zmm1,zmm1,zmm4
0x00007f74a86fa154: vaddps zmm1,zmm1,zmm2
0x00007f74a86fa15a: vaddps zmm1,zmm1,zmm0
0x00007f74a86fa160: add r8d,0x40
0x00007f74a86fa164: cmp r8d,r11d
0x00007f74a86fa167: jl 0x00007f74a86fa0f0We're using more registers and instructions per iteration. Nice! And what's more, our Lucene code hand unrolls the loop too, by another 4x (hmm... that's a lot of unrolling).
So, is it fast?
To assess the impact of rewriting such low-level operations, we turn to JMH, which is the generally accepted way to perform microbenchmarks of such Java code. Here we used Robert Muir's very nice and convenient set of benchmarks that allowed us to quickly compare before and after code variants.
Remember, SIMD offers data parallelism, so the more data we're processing the greater the potential benefit. In our case, this directly relates to the dimension size of our vectors — we expect to see bigger benefits for larger dimension sizes. Let's look at the floating-point variant of dot product with vectors of 1024 dimensions, when run on a CPU that supports AVX 512; Intel Core i9-11900F @ 2.50GHz:
Benchmark (size) Mode Cnt Score Error Units
FloatDotProductBenchmark.dotProductNew 1024 thrpt 5 25.657 ± 2.105 ops/us
FloatDotProductBenchmark.dotProductOld 1024 thrpt 5 3.320 ± 0.079 ops/usThe benchmark measures operations per microsecond, so larger is better. Here we see that the new dot product executes approximately eight times faster than the old one. And we see similar performance gains across the different low-level primitive operations, both for float and binary:
Benchmark (size) Mode Cnt Score Error Units
BinaryCosineBenchmark.cosineDistanceNew 1024 thrpt 5 10.637 ± 0.068 ops/us
BinaryCosineBenchmark.cosineDistanceOld 1024 thrpt 5 1.115 ± 0.008 ops/us
BinaryDotProductBenchmark.dotProductNew 1024 thrpt 5 22.050 ± 0.007 ops/us
BinaryDotProductBenchmark.dotProductOld 1024 thrpt 5 3.349 ± 0.041 ops/us
BinarySquareBenchmark.squareDistanceNew 1024 thrpt 5 16.215 ± 0.129 ops/us
BinarySquareBenchmark.squareDistanceOld 1024 thrpt 5 2.479 ± 0.032 ops/us
FloatCosineBenchmark.cosineNew 1024 thrpt 5 9.394 ± 0.048 ops/us
FloatCosineBenchmark.cosineOld 1024 thrpt 5 0.750 ± 0.002 ops/us
FloatDotProductBenchmark.dotProductNew 1024 thrpt 5 25.657 ± 2.105 ops/us
FloatDotProductBenchmark.dotProductOld 1024 thrpt 5 3.320 ± 0.079 ops/us
FloatSquareBenchmark.squareNew 1024 thrpt 5 19.437 ± 0.122 ops/us
FloatSquareBenchmark.squareOld 1024 thrpt 5 2.355 ± 0.003 ops/usWe see significant improvements across all primitive operation variants and also with various small to large dimension sizes (this is not shown here, but it can be seen in the Lucene PR). This is all great, but how does this relate to higher-level workloads?
Zooming out
Microbenchmarks are important to understand how low-level primitive operations are performing, but how does this impact at the macro level? For that, we can look at the vector search benchmarks that we have for Elasticsearch®, namely SO Vector and Dense Vector. Both benchmarks show significant improvements, but let's look at SO Vector as it is more interesting since it has higher vector dimensions than Dense Vector.
The SO Vector benchmark tests vector search performance with 2 million vectors of 768 dimensions and kNN with filtering. The vectors are based on a data set derived from a dump of StackOverflow posts. Elasticsearch runs on GCP using a single-node cluster, running on a custom n2 instance with 8 vCPUs, 16GB RAM, and 1x300GiB SSD disk. The node has a CPU platform pinned to Ice Lake.
There's quite a lot of pre-existing variance in the benchmark, but overall we see positive improvement:
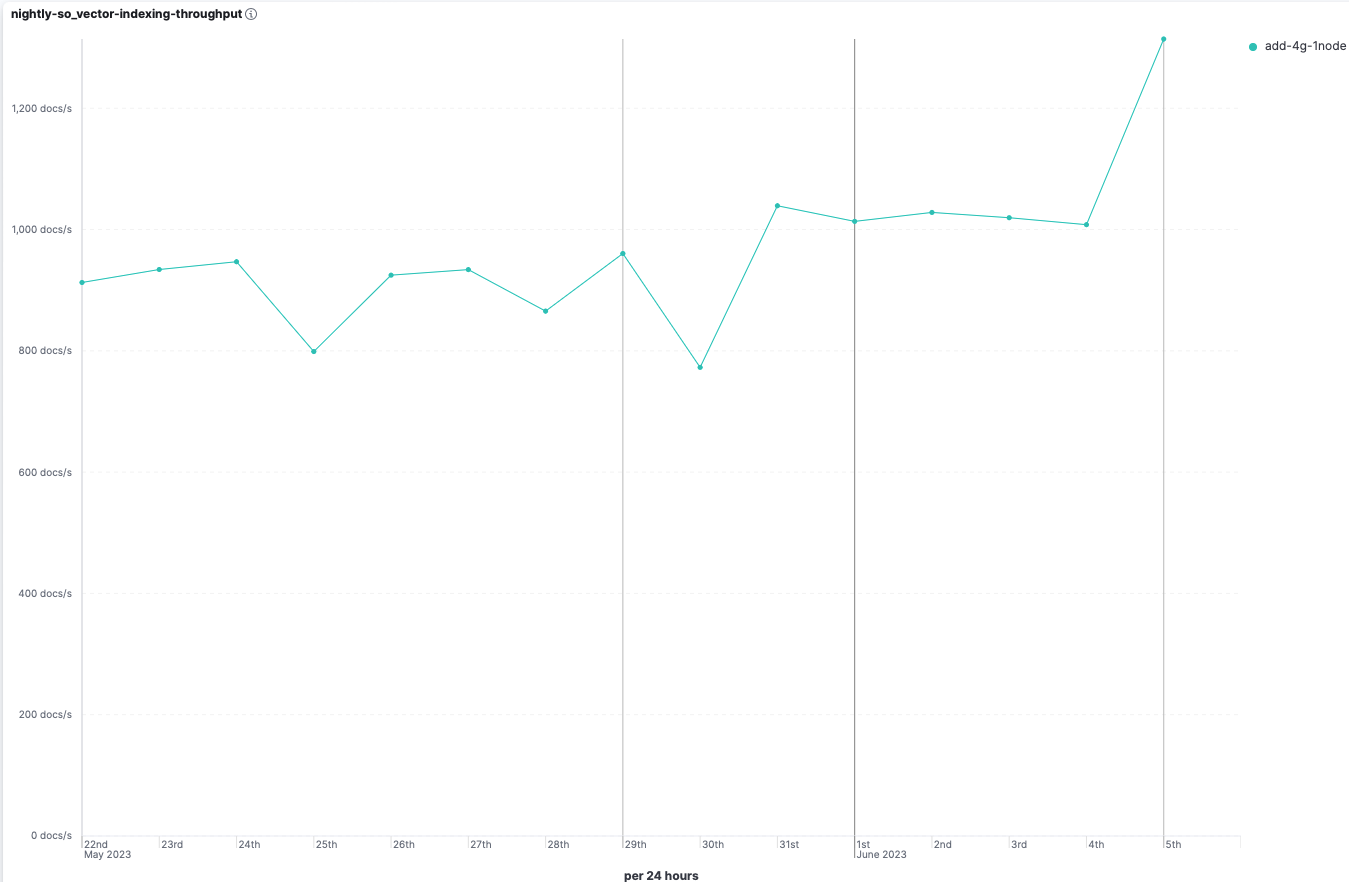
- Indexing throughput improved by ~30%.
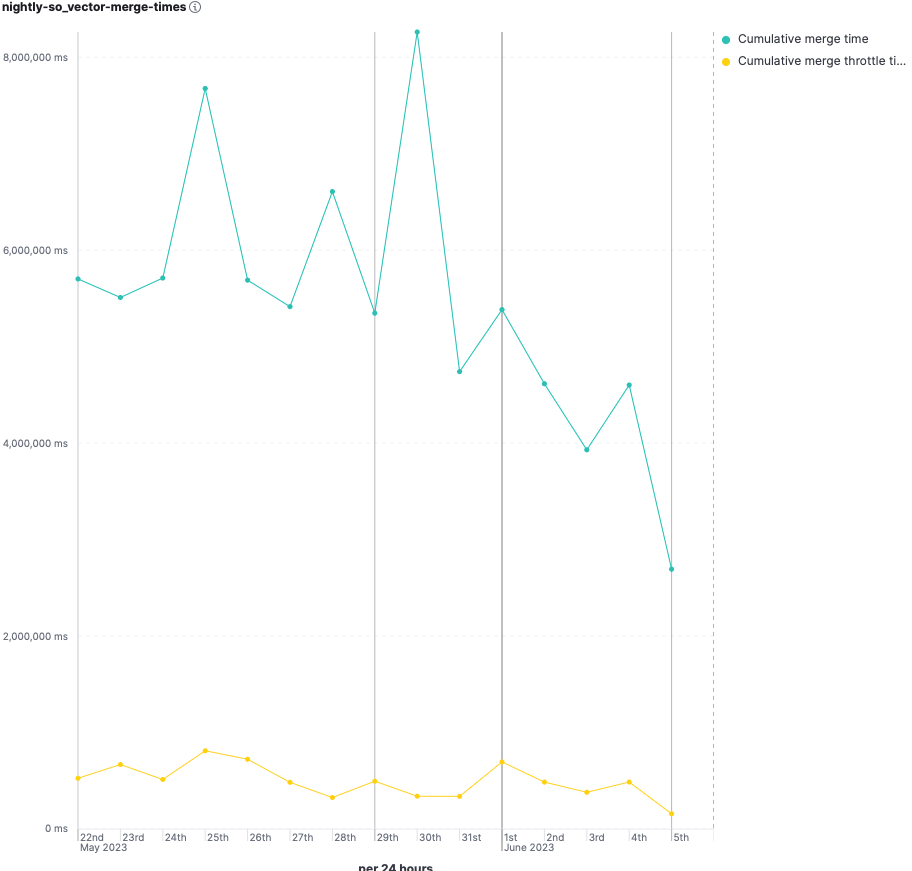
- Merge time decreased by ~40%.
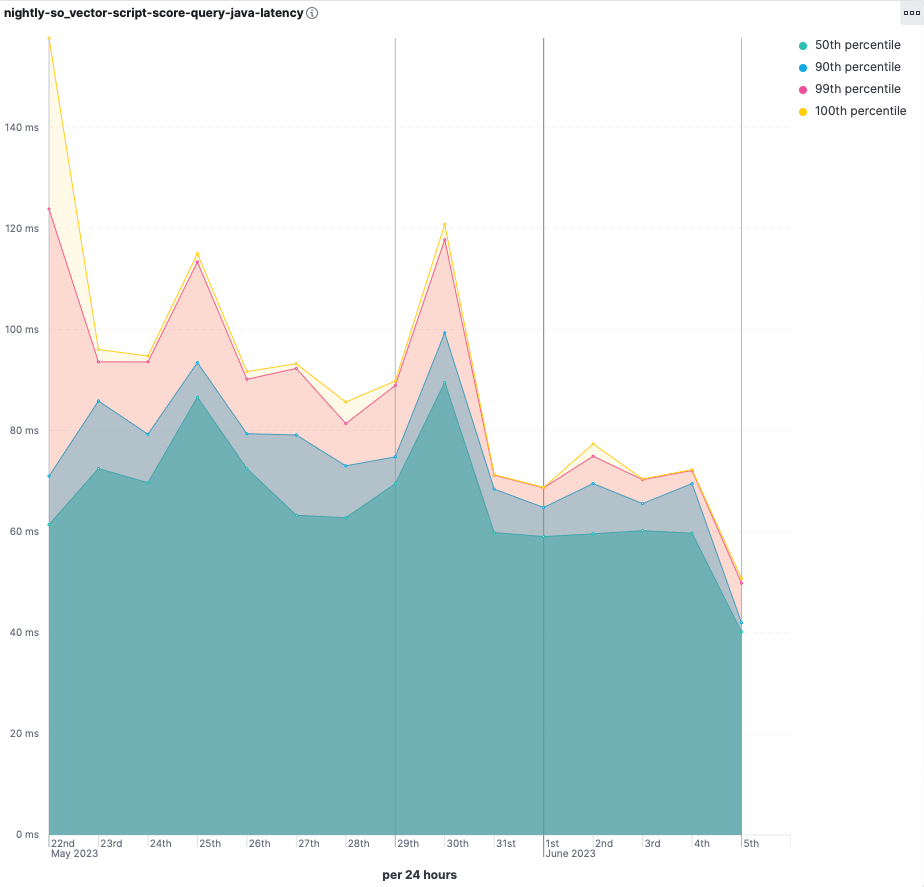
- Query latencies improved significantly.
But isn't the Panama Vector API incubating?
The JDK Vector API, being developed in Project Panama, has been incubating for quite a while now. The incubating status is not a reflection of its quality, but more a consequence of a dependency on other exciting work happening in OpenJDK, namely value types. Lucene is forging the way here, on the "bleeding edge," and has a novel way of leveraging non-final APIs in the JDK — by building against an "apijar" containing the JDK-version specific APIs — thanks Uwe. This is a pragmatic approach that we don't take lightly. As with most things in life, it's a tradeoff. We only consider adopting non-final JDK APIs when the potential benefits outweigh the maintenance cost.Lucene still has the scalar variants of these low-level primitive operations. The version of the implementation is selectable at startup (see the Lucene change log). The faster Panama implementation is available on JDK 20 and the upcoming JDK 21, while we fallback to the scalar implementation for older JDKs, or when otherwise not available. Again, support for only the latest JDK versions is a pragmatic choice when balancing potential benefits versus maintenance cost.
Wrapping up
We can now write Java code that reliably leverages hardware accelerated SIMD instructions by using the Panama Vector API. In Lucene 9.7.0, we added the ability to enable an alternative faster implementation of the low-level primitive operations used by Vector Search. Elasticsearch 8.9.0 has enabled this faster implementation by default out of the box, so you get the improved performance benefits without having to do anything. We see significant performance improvements in our vector search benchmarks and fully expect this to translate to user workloads.
SIMD instructions are not new and have been around for a long time. As always, you need to do your own performance benchmarking to see the effects that this will have in your environment. AVX 512 is cool, but it can suffer from the dreaded "downclocking." Overall, we see positive improvements across the board from this change.
Finally, I'd like to call out Lucene PMC members Robert Muir and Uwe Schindler, for the enjoyable and productive collaboration that led to this improvement, and without whom this would not have happened.