¿Qué es kNN?
Definición de k vecino más cercano
kNN, o el algoritmo del vecino más cercano, es un algoritmo de machine learning que usa la proximidad para comparar un punto de datos con un set de datos con el que se entrenó y que memorizó para hacer predicciones. Este aprendizaje basado en instancias le otorga a kNN la denominación de "aprendizaje vago" y permite que el algoritmo lleve a cabo problemas de clasificación o regresión. kNN funciona bajo el supuesto de que se pueden encontrar puntos similares cerca unos de otros: cada oveja con su pareja.
Como algoritmo de clasificación, kNN asigna un nuevo punto de datos al set de mayoría entre sus vecinos. Como algoritmo de regresión, kNN hace una predicción basada en el promedio de los valores más cercanos al punto de búsqueda.
kNN es un algoritmo de aprendizaje supervisado en el que "k" representa la cantidad de vecinos más cercanos considerados en el problema de clasificación o regresión, y "NN" se refiere a los vecinos más cercanos a la cantidad elegida para k.
Breve historia del algoritmo de kNN
kNN fue desarrollado por primera vez por Evelyn Fix y Joseph Hodges en 1951 en el contexto de una investigación realizada para el ejército de los Estados Unidos.1 Explicaron en una publicación el análisis discriminante, que es un método de clasificación no paramétrico. En 1967, Thomas Cover y Peter Hart ampliaron el método de clasificación no paramétrico y publicaron su artículo "Nearest Neighbor Pattern Classification" (Clasificación de patrones de vecino más cercano)2. Casi 20 años después, el algoritmo fue perfeccionado por James Keller, quien desarrolló un "KNN difuso" que produce tasas de error más bajas.3
En la actualidad, el algoritmo de kNN es el algoritmo más usado, gracias a su adaptabilidad para la mayoría de los campos, desde la genética hasta las finanzas y el servicio al cliente.
¿Cómo funciona kNN?
El algoritmo de kNN funciona como un algoritmo de aprendizaje supervisado, lo que significa que se alimenta con sets de datos de entrenamiento que memoriza. Depende de estos datos de entrada etiquetados para aprender una función que produzca una salida adecuada cuando se le dan nuevos datos sin etiquetar.
Esto permite al algoritmo resolver problemas de clasificación o regresión. Si bien el cálculo de kNN se realiza durante una búsqueda y no durante una fase de entrenamiento, tiene requisitos de almacenamiento de datos importantes y, por lo tanto, depende en gran medida de la memoria.
Con respecto a los problemas de clasificación, el algoritmo de KNN asignará una etiqueta de clase basada en una mayoría, lo que significa que usará la etiqueta que se encuentra presente con mayor frecuencia en torno a un punto de datos determinado. En otras palabras, la salida de un problema de clasificación es el modo de los vecinos más cercanos.
Una diferencia: votación por mayoría frente a votación por pluralidad
La votación por mayoría indica que cualquier resultado por encima del 50 % es la mayoría. Esto se aplica si hay dos etiquetas de clase en consideración. Sin embargo, el voto por pluralidad aplica si se están considerando varias etiquetas de clase. En estos casos, cualquier resultado por encima del 33.3 % sería suficiente para indicar una mayoría y, por lo tanto, para brindar una predicción. Entonces, el voto por pluralidad es un término más preciso para definir el modo de kNN.
Si tuviéramos que ilustrar esta diferencia:
Una predicción binaria
Y: 🎉 🎉 🎉 ❤️❤️❤️❤️❤️
Voto por mayoría: ❤️
Voto por pluralidad: ❤️
Una configuración de varias clases
Y: ⏰⏰⏰💰💰💰🏠🏠🏠🏠
Voto por mayoría: Ninguna
Voto por pluralidad: 🏠
Los problemas de regresión usan el promedio de los vecinos más cercanos para predecir una clasificación. Un problema de regresión generará números reales como salida de la consulta.
Por ejemplo, si estuvieras haciendo un gráfico para predecir el peso de alguien según su altura, los valores que indican la altura serían independientes, mientras que los valores de peso serían dependientes. Al realizar un cálculo de la razón altura-peso promedio, podrías calcular el peso de alguien (la variable dependiente) según su altura (la variable independiente).
Cuatro formas de computar las métricas de distancia de kNN
La clave para el algoritmo de kNN es determinar la distancia entre el punto de búsqueda y los otros puntos de datos. Determinar las métricas de distancia posibilita los límites de decisión. Estos límites crean diferentes regiones de puntos de datos. Existen distintos métodos que se usan para calcular la distancia:
- La distancia euclidiana es la medida de distancia más común, que mide una línea recta entre el punto de búsqueda y el otro punto que se está midiendo.
- La distancia de Manhattan también es una medida de distancia popular, que mide el valor absoluto entre dos puntos. Se representa en una cuadrícula y, con frecuencia, se la llama geometría de taxi; ¿cómo viajas del punto A (tu punto de búsqueda) al punto B (el punto que se está midiendo)?
- La distancia de Minkowski es una generalización de las métricas de distancia euclidiana y de Manhattan, que te permite crear otras métricas de distancia. Se calcula en un espacio vectorial normalizado. En la distancia de Minkowski, p es el parámetro que define el tipo de distancia que se usa en el cálculo. Si p=1, se usa la distancia de Manhattan. Si p=2, entonces se usa la distancia euclidiana.
- La distancia de Hamming, también conocida como métrica de superposición, es una técnica que se utiliza con vectores booleanos o de cadena para identificar los lugares en los que los vectores no coinciden. En otras palabras, mide la distancia entre dos cadenas de igual longitud. Es particularmente útil para los códigos de detección y corrección de errores.
Cómo elegir el mejor valor k
Para elegir el mejor valor k (la cantidad de vecinos más cercanos que se considera), debes experimentar con algunos valores para encontrar el valor k que genere las predicciones más exactas con la menor cantidad de errores. Determinar el mejor valor es un ejercicio de equilibrio:
- Los valores k bajos hacen que las predicciones sean inestables.
Toma este ejemplo: un punto de búsqueda está rodeado por 2 puntos verdes y un triángulo rojo. Si k=1 y el punto más cercano al punto de búsqueda es uno de los puntos verdes, el algoritmo predecirá incorrectamente un punto verde como el resultado de la búsqueda. Los valores k bajos tienen alta varianza (el modelo se ajusta demasiado a los datos de entrenamiento), alta complejidad y bajo sesgo (el modelo es lo suficientemente complejo como para ajustarse bien a los datos de entrenamiento). - Los valores k altos son ruidosos.
Un valor k más alto aumentará la precisión de las predicciones porque hay más números a partir de los cuales calcular los modos o promedios. Sin embargo, si el valor k es demasiado alto, probablemente dará como resultado una varianza baja, complejidad baja y sesgo alto (el modelo NO es lo suficientemente complejo como para ajustarse bien a los datos de entrenamiento).
Lo ideal es encontrar un valor k que se encuentre entre varianza alta y sesgo alto. También se recomienda elegir un número impar para k, a fin de evitar empates en el análisis de clasificación.
El valor k correcto también es relativo al set de datos. Para elegir ese valor, puedes intentar encontrar la raíz cuadrada de N, donde N es el número de puntos de datos en el set de datos de entrenamiento. Las tácticas de validación cruzada también pueden ayudarte a elegir el valor k más adecuado para el set de datos.
Ventajas del algoritmo de kNN
El algoritmo de kNN suele describirse como el algoritmo de aprendizaje supervisado "más simple", lo cual lleva a sus diversas ventajas:
- Simple: kNN es fácil de implementar por lo simple y preciso que es. Como tal, suele ser uno de los primeros clasificadores que aprende un científico de datos.
- Adaptable: Tan pronto se agregan nuevas muestras de entrenamiento a su set de datos, el algoritmo de kNN ajusta sus predicciones para incluir los datos de entrenamiento nuevos.
- Fácil de programar: kNN requiere solo algunos hiperparámetros: un valor k y una métrica de distancia. Esto hace que sea un algoritmo relativamente poco complicado.
Además, el algoritmo de kNN no requiere tiempo de entrenamiento, ya que almacena los datos de entrenamiento, y su potencia de procesamiento solo se usa al realizar predicciones.
Desafíos y limitaciones de kNN
Si bien el algoritmo de kNN es simple, también presenta un conjunto de desafíos y limitaciones que se deben, en parte, a su simpleza:
- Difícil de escalar: Dado que KnN ocupa mucha memoria y almacenamiento de datos, eleva los gastos asociados con el almacenamiento. Esta dependencia de la memoria también significa que el algoritmo es intensivo en cuanto al procesamiento, lo que a su vez requiere muchos recursos.
- Maldición de la dimensionalidad: Se refiere a un fenómeno que se produce en informática, en el que un conjunto fijo de ejemplos de entrenamiento se ve desafiado por una cantidad creciente de dimensiones y el aumento inherente de los valores de las características en estas dimensiones. En otras palabras, los datos de entrenamiento del modelo no pueden seguir el ritmo de la dimensionalidad en evolución del hiperespacio. Esto significa que las predicciones se vuelven menos precisas porque la distancia entre el punto de consulta y los puntos similares se hace más amplia, en otras dimensiones.
- Sobreajuste: El valor de k, como se mostró anteriormente, afectará el comportamiento del algoritmo. Esto puede suceder, especialmente, cuando el valor de k es demasiado bajo. Los valores de k más bajos pueden sobreajustar los datos, mientras que los valores de k más altos "suavizarán" los valores de predicción porque el algoritmo promedia los valores de una zona más amplia.
Principales casos de uso de kNN
El algoritmo de kNN, popular por su simpleza y precisión, tiene una variedad de aplicaciones, en especial cuando se usa para análisis de clasificación.
- Clasificación de relevancia: kNN usa algoritmos de procesamiento de lenguaje natural (NLP) para determinar qué resultados son más relevantes para una consulta.
- Búsqueda por similitud de imágenes o videos: La búsqueda por similitud de imágenes usa descripciones en lenguaje natural para encontrar imágenes que coincidan con búsquedas de texto.
- Reconocimiento de patrones: kNN se puede usar para identificar patrones en la clasificación de dígitos o texto.
- Finanzas: En el sector financiero, KnN se puede usar para la previsión del mercado de valores, los tipos de cambio de divisas, etc.
- Recomendaciones de productos y motores de recomendaciones: ¡Piensa en Netflix! " Si te gustó esto, creemos que también te gustará... ". Cualquier sitio que use una versión de esa frase, abiertamente o no, probablemente esté usando un algoritmo kNN para alimentar su motor de recomendaciones.
- Salud: En el campo de la medicina y la investigación médica, el algoritmo kNN se puede usar en genética para calcular la probabilidad de ciertas expresiones genéticas. Esto permite a los médicos predecir la probabilidad de cáncer, ataques cardíacos o cualquier otra afección hereditaria.
- Preprocesamiento de datos: El algoritmo kNN se puede usar para calcular los valores que faltan en los sets de datos.
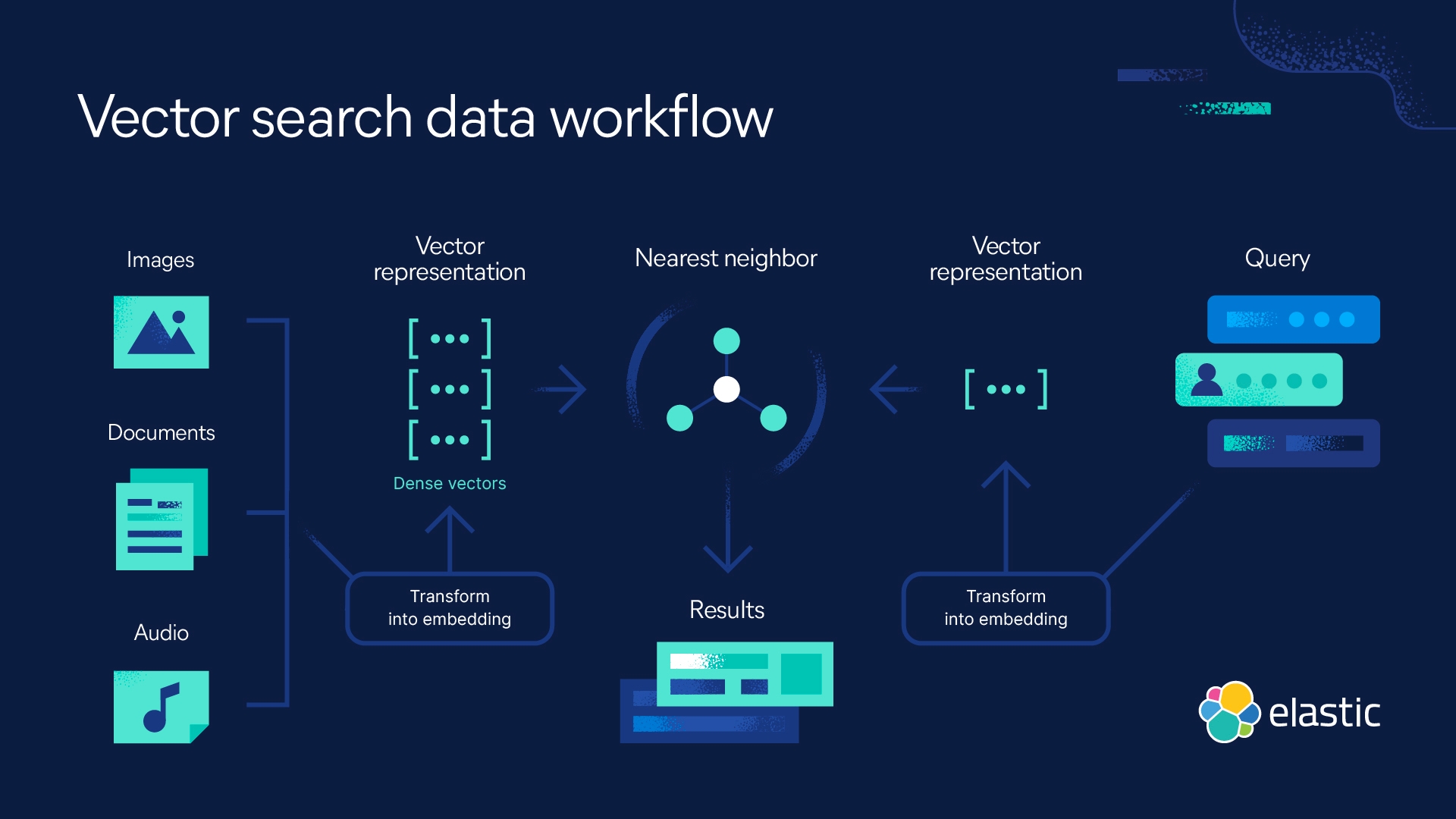
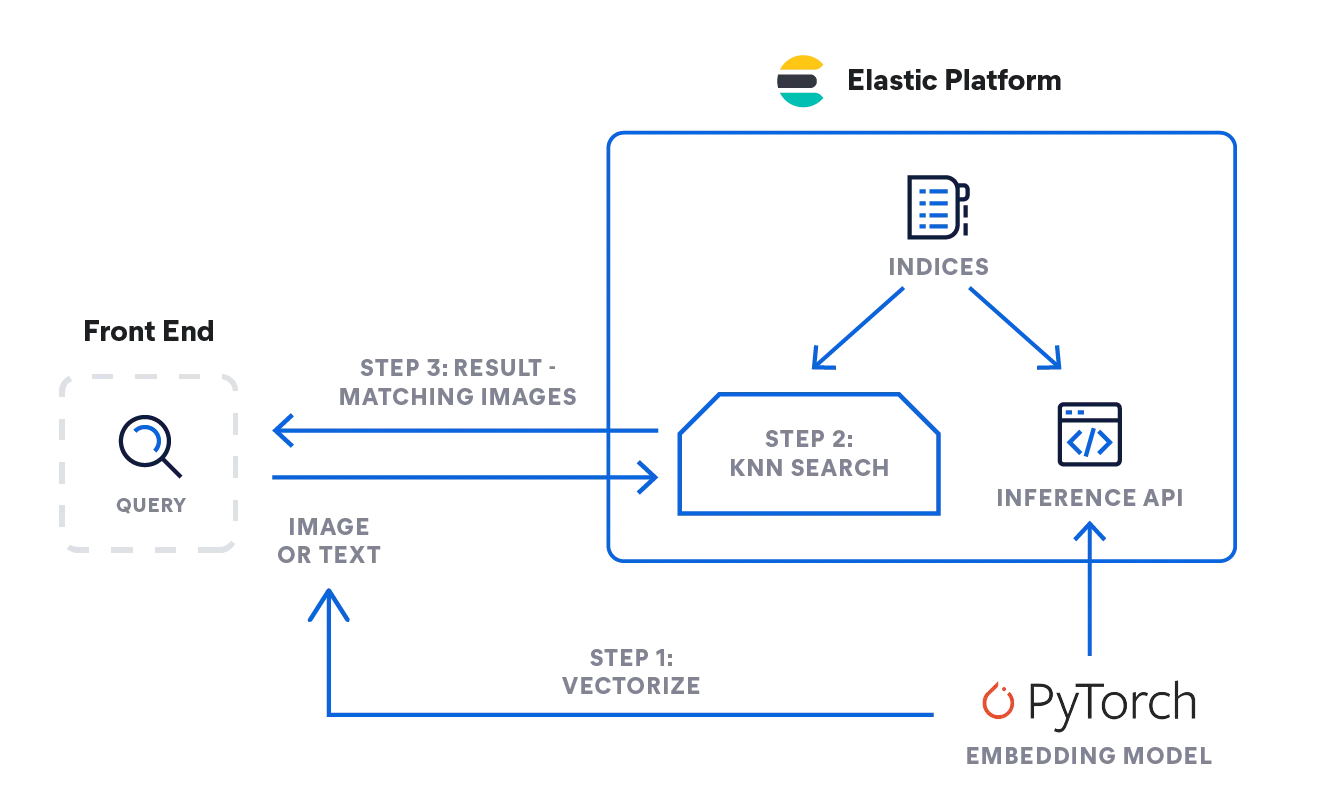
Búsqueda de kNN con Elastic
Elasticsearch te permite implementar la búsqueda de kNN. Se admiten dos métodos: kNN aproximado y kNN exacto de fuerza bruta. Puedes usar la búsqueda de kNN en el contexto de búsqueda por similitud, clasificación de relevancia basada en algoritmos de NLP y recomendaciones de productos y motores de recomendaciones.
Preguntas frecuentes sobre los k vecinos más cercanos
¿Cuándo usar kNN?
Usa kNN para hacer predicciones basadas en similitudes. Así, puedes usar kNN para la clasificación de relevancia en el contexto de algoritmos de procesamiento de lenguaje natural, para motores de recomendaciones y búsqueda por similitudes, o recomendaciones de productos. Ten en cuenta que kNN es útil cuando tienes un sets de datos relativamente pequeño.
¿kNN es machine learning supervisado o no supervisado?
kNN es machine learning supervisado. Se lo alimenta con un set de datos que almacena y solo procesa los datos cuando se realizan consultas.
¿Qué significa kNN?
kNN significa algoritmo de k vecino más cercano, en donde k indica la cantidad de vecinos más cercanos que se consideraron en el análisis.
Notas al pie
- Silverman, B. W. y Jones, M. C. (1989). E. Fix y J. L. Hodes (1951): An Important Contribution to Nonparametric Discriminant Analysis and Density Estimation: Commentary on Fix and Hodges (Una contribución importante al análisis discriminante no paramétrico y la estimación de densidad: comentario sobre Fix y Hodges) (1951). International Statistical Institute (ISI) / Revue Internationale de Statistique,57(3), 233–238. https://doi.org/10.2307/1403796
- T. Cover y P. Hart, "Nearest neighbor pattern classification" (Clasificación de patrones del vecino más cercano), en IEEE Transactions on Information Theory, vol. 13, núm. 1, págs. 21-27, enero de 1967, doi: 10.1109/TIT.1967.1053964. https://ieeexplore.ieee.org/document/1053964/authors#authors
- K-Nearest Neighbors Algorithm: Classification and Regression Star, History of Data Science (Algoritmo de los vecinos más cercanos: estrella de clasificación y regresión, historia de la ciencia de datos, Consultado: 23/10/2023, https://www.historyofdatascience.com/k-nearest-neighbors-algorithm-classification-and-regression-star/