什么是 kNN?
K 最近邻的定义
kNN 又称为 k 最近邻算法,是一种 Machine Learning 算法,会使用临近度来将一个数据点与训练时所使用并已记住的一个数据集进行对比,从而做出预测。这种基于实例的学习使 kNN 赢得了“惰性学习”的名称,并让人们能够使用此算法解决分类或回归问题。kNN 算法的工作原理是假设相似的数据点会彼此靠近,即物以类聚。
作为一种分类算法,kNN 将新的数据点分配给其邻居中占多数的集合。作为一种回归算法,kNN 根据最接近查询点的值的平均值进行预测。
kNN 是一种监督式学习算法,其中的字母 k 表示在分类或回归问题中所考虑的最近邻的数量,NN 代表为 k 所选的数字的最近邻。
kNN 算法的简短历史
kNN 最初是由 Evelyn Fix 和 Joseph Hodges 于 1951 年开发的,当时他们正在为美国军方进行研究1。他们发表了一篇论文来解释判别分析(非参数分类方法的一种)。在 1967 年,Thomas Cover 和 Peter Hart 在非参数分类方法的基础上进行扩展,发表了论文“最近邻模式分类”2。大约 20 年后,James Keller 对此算法进行了优化,并开发出了“模糊 KNN”,这种方法的错误率较低3。
现在,kNN 算法是使用最为广泛的算法,因为它的可调整性特别强,适用于大部分行业(从遗传学,到金融和客户服务,不一而足)。
kNN 的工作原理是什么?
kNN 算法是一种监督式学习算法,意味着您需要为其提供训练数据,然后算法会记住这些数据。它依赖于此已添加标签的输入数据来学习功能,并在收到未添加标签的新数据时,通过此功能来生成正确的输出。
这能够支持算法解决分类或回归问题。虽然 kNN 的计算过程是在查询时完成,而不是在训练阶段完成,但是它有重要的数据存储要求,因此十分依赖于内存。
对于分类问题,kNN 会基于多数值分配一个类别标签,这意味着它会使用在给定的数据点周围最频繁出现的标签。换言之,分类问题的输出是最近邻中的众数。
区别:多数投票和相对多数投票的区别
多数投票表示只要超过 50% 就为多数。如果考虑范围内只有两个类别标签,则适用此种投票。然而,如果考虑范围内有多于两个类别标签,则适用相对多数投票。在这些情况下,只要超过 33.3%,就可充分表示获得了多数投票,因此能够提供预测。因此,相对多数投票是用来描述 kNN 众数的更为准确的词汇。
如果我们要解释这一区别:
二元预测
Y: 🎉🎉🎉❤️❤️❤️❤️❤️
多数投票:❤️
相对多数投票:❤️
多类别设置
Y: ⏰⏰⏰💰💰💰🏠🏠🏠🏠
多数投票:无
相对多数投票:🏠
回归问题会使用最近邻的平均值来预测分类。回归问题会产生一个实数作为查询的输出。
例如,如果您要制作一份图表,以便基于某人的身高来预测其体重,则表示身高的值将会是独立的,而体重值是非独立的。通过计算身高与体重比值的平均值,您可以基于某人的身高(独立变量)估测其体重(非独立变量)。
kNN 距离指标的 4 种计算方法
kNN 算法的关键是确定查询点与其他数据点之间的距离。通过确定距离指标,您能够确定决策边界。这些边界会生成不同的数据点区域。您可以通过不同方法来计算距离:
- 欧几里得距离是最常见的距离度量,测量的是查询点和被测量的其他数据点之间的直线距离。
- 曼哈顿距离也是一个特别热门的距离度量,测量的是两点之间的绝对值。它会在网格上进行表示,通常被称为计程车几何,亦即您如何从 A 点(您的查询点)到达 B 点(被测量的点)?
- 闵可夫斯基距离是欧几里得和曼哈顿距离指标的广义形式,支持创建其他距离指标。您可以在标准化矢量空间中计算此距离。在闵可夫斯基距离中,p 是定义计算时所用距离类型的参数。如果 p=1,则使用曼哈顿距离。如果 p=2,则使用欧几里得距离。
- 汉明距离也称为重叠指标,这种方法通常与布尔或字符串矢量一起使用,从而识别哪里的矢量不匹配。换言之,它衡量的是两个相同长度的字符串之间的距离。对于错误检测和错误更正代码,这一方法尤其有用。
如何选择最佳的 k 值
如要选择最佳的 k 值(所考虑的最近邻的数量),您必须使用几个值进行试验,以找到能够在错误数量最少的前提下产生最准确预测的 k 值。确定最佳值需要平衡多方面因素:
- 低 k 值会让预测变得不稳定。
举个例子,一个查询点被两个绿点和一个红三角包围。如果 k=1,而且与查询点最接近的点恰巧是绿点中的一个,则算法将无法正确预测,会说查询结果为绿点。低 k 值表示高方差(模型与训练数据过于契合)、高复杂性和低偏见(模型足够复杂,能够很好地契合训练数据)。 - 高 k 值会产生噪音。较高的 k 值会提高预测的准确性,因为计算众数或平均数时所使用的数字更多。然而,如果 k 值过高,这可能会导致低方差、低复杂度和高偏见(模型复杂度不够,不能很好地契合训练数据)。
理想状况是,您需要找到一个介于高方差和高偏见之间的值。我们还建议您为 k 选择奇数,从而避免在分类分析中出现平局情况。
正确的 k 值与您的数据集也有关系。要选择该值,您可能要尝试找到 N 的平方根,此处 N 是训练数据集中数据点的数量。交叉验证也可以帮助您选择最适合数据集的 k 值。
kNN 算法的优势
kNN 算法通常被称作“最简单的”监督式学习算法,所以它有多项优势:
- 简单:kNN 很容易部署,因为它既简单又准确。所以,它通常是数据科学家学习的第一批分类器之一。
- 适应性:用户向数据集添加新的训练样本后,kNN 算法会调整其预测以将新训练数据也包括进去。
- 可轻松编程:kNN 只要求几个超级参数:一个 k 值和一个距离指标。这使得其成为一个相当简单的算法。
此外,kNN 算法不要求预留出训练时间,因为它会存储训练数据,并且只有在进行预测时才会使用其计算能力。
kNN 的挑战和局限性
kNN 算法固然很简单,但也正是由于这一简单性,它也面临着一系列挑战和局限性:
- 难以扩展:因为 kNN 会占用大量内存和数据存储空间,所以它会抬高与存储相关的费用。对内存的这一依赖也意味着这一算法是计算密集型任务,所以相应地也是资源密集型任务。
- 维度灾难:这指的是发生在计算机科学领域的下列现象:因为维数越来越多,而且这些维度中的特征值会有内在增加,所以固定的训练示例集受到挑战。换言之,此模型的训练数据无法跟上超级空间不断发展的维数。这意味着预测的准确性变低了,因为在其他维度上,查询点和相似点之间的距离变宽了。
- 过拟合:如前面所示,k 值会影响算法的行为。当 k 值过低时,尤其会发生这种情况。k 值较低会导致算法与数据过拟合,而 k 值较高会让预测值“变得平滑”,因为算法会在更大的区域内对值求平均数。
kNN 主要用例
因为 kNN 算法使用简单且结果准确,所以很热门,有很多应用场景,尤其会用于分类分析。
- 相关性排序:kNN 使用自然语言处理 (NLP) 算法来确定哪个结果与查询最相关。
- 图像或视频的相似性搜索:图像相似性搜索会使用自然语言描述来查找与文本查询相匹配的图像。
- 模式识别:kNN 可用来在文本或数字分类问题中识别模式。
- 金融:在金融领域,kNN 可用于股票市场预测、货币汇率预测等。
- 产品推荐和推荐引擎:想想 Netflix!“如果您喜欢此内容,我们猜您也会喜欢……”任何(公开或非公开)使用这句话类似版本的网站都很可能在使用 kNN 算法来为其推荐引擎提供支持。
- 医疗保健:在药物和医学研究领域,kNN 算法可用于遗传学中,以计算特定基因表达的概率。借助这一方法,医生可以预测癌症、心脏病或任何其他遗传疾病的可能性。
- 数据预处理:kNN 算法可用来预测数据集中的缺失值。
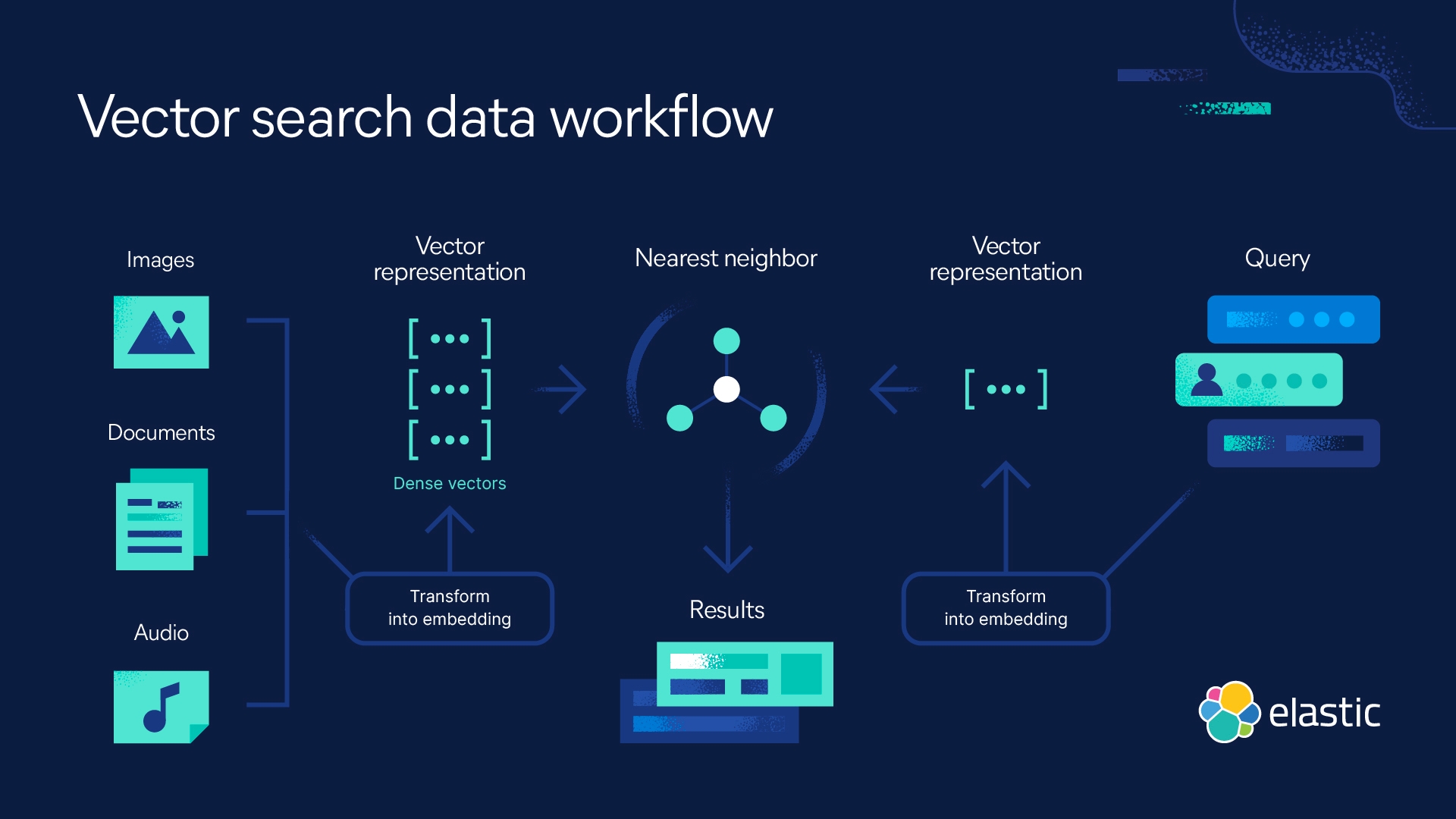
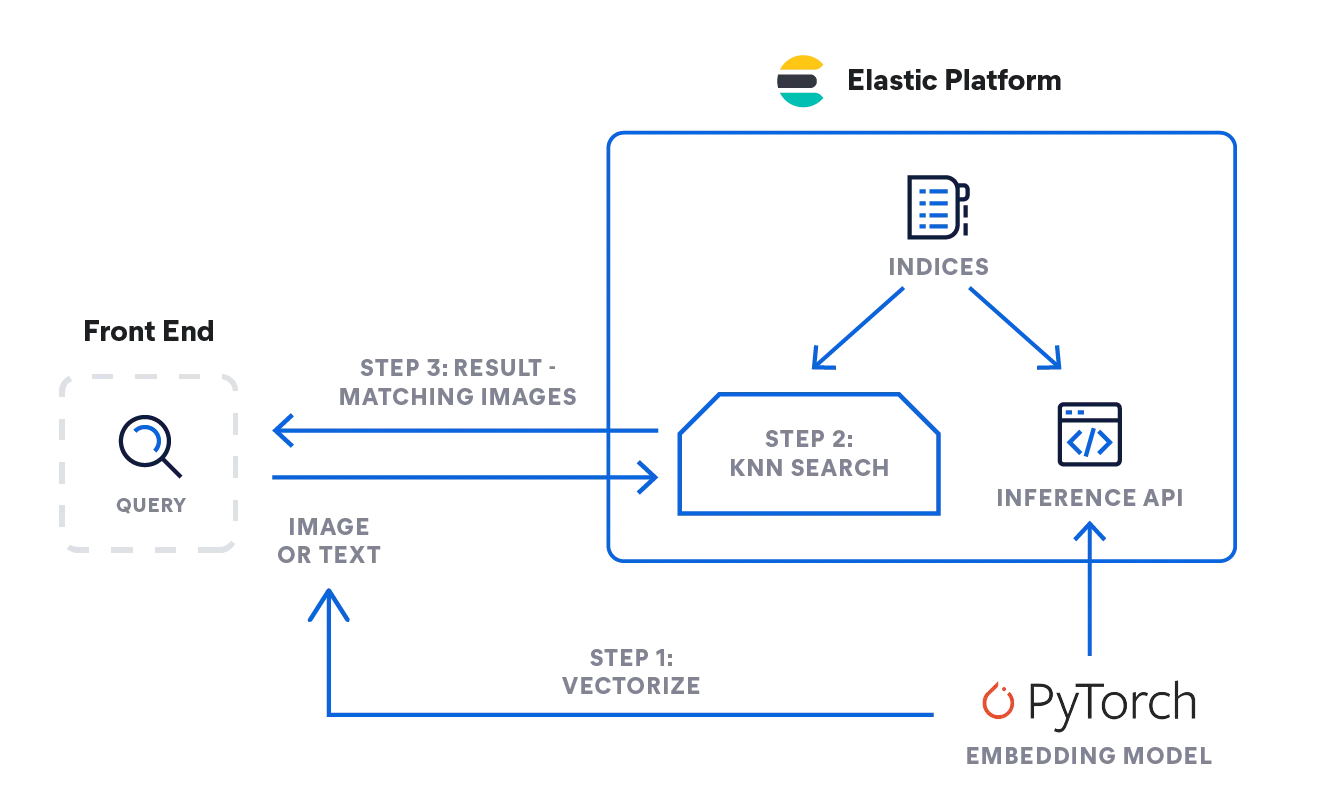
使用 Elastic 实现 kNN 搜索
Elasticsearch 支持您实施 kNN 搜索。其支持两种方法:近似 kNN 和精准的暴力 kNN.您可以在相似性搜索、基于 NLP 算法的相关性排序以及产品推荐和推荐引擎等场景中使用 kNN 搜索。
K 最近邻常见问题解答
何时使用 kNN?
利用 kNN 算法来基于相似性做出预测。因此,在自然语言处理算法的背景下,您可以针对相似性搜索和推荐引擎或者产品推荐,使用 kNN 进行相关性排序。请注意,当您拥有相对较小的数据集时,kNN 可以发挥作用。
kNN 是监督式还是非监督式机器学习?
kNN 是监督式机器学习。人们需要为此算法提供一个数据集,然后此算法会存储该数据集,并且只有在查询该数据集时才会对其进行处理。
kNN 表示什么意思?
kNN 表示 k 最近邻算法,其中的 k 表示在分析过程中所考虑的最近邻的数量。
脚注
- Silverman, B.W., & Jones, M.C. (1989). E. Fix and J.L Hodes (1951): An Important Contribution to Nonparametric Discriminant Analysis and Density Estimation: Commentary on Fix and Hodges (1951). International Statistical Institute (ISI) / Revue Internationale de Statistique,57(3), 233–238. https://doi.org/10.2307/1403796
- T. Cover and P. Hart, "Nearest neighbor pattern classification," in IEEE Transactions on Information Theory, vol. 13, no. 1, pp. 21-27, January 1967, doi: 10.1109/TIT.1967.1053964. https://ieeexplore.ieee.org/document/1053964/authors#authors
- K 最近邻算法:分类和回归之星,History of Data Science,访问时间:2023 年 10 月 23 日,https://www.historyofdatascience.com/k-nearest-neighbors-algorithm-classification-and-regression-star/