Von der Vektorsuche bis hin zu leistungsstarken REST-APIs bietet Elasticsearch Entwicklern das umfangreichste Such-Toolkit. Sehen Sie sich die Beispiel-Notebooks auf GitHub an, um etwas Neues testen. Sie können auch noch heute Ihre kostenlose Testversion starten oder Elasticsearch lokal ausführen.
In der Vergangenheit haben wir einige der Herausforderungen erörtert , die mit der Suche in mehreren HNSW-Graphen einhergehen, und wie wir diese bewältigen konnten. Damals deuteten wir einige weitere Verbesserungen an, die wir geplant hatten. Dieser Beitrag ist der Höhepunkt dieser Arbeit.
Sie fragen sich vielleicht, warum Sie überhaupt mehrere Diagramme verwenden? Dies ist ein Nebeneffekt einer Architekturentscheidung in Lucene: unveränderliche Segmente. Wie bei den meisten architektonischen Entscheidungen gibt es Vor- und Nachteile. Beispielsweise haben wir vor Kurzem Serverless Elasticsearch allgemein zugänglich gemacht. In diesem Zusammenhang haben wir durch unveränderliche Segmente erhebliche Vorteile erzielt, darunter eine effiziente Indexreplikation und die Möglichkeit, die Index- und Abfrageberechnung zu entkoppeln und unabhängig voneinander automatisch zu skalieren. Bei der Vektorquantisierung bieten uns Segmentzusammenführungen die Möglichkeit, Parameter zu aktualisieren, um sie an die Dateneigenschaften anzupassen. In diesem Sinne sind wir der Meinung, dass die Möglichkeit, Datenmerkmale zu messen und Indexierungsentscheidungen zu überprüfen, noch weitere Vorteile mit sich bringt.
In diesem Beitrag besprechen wir die Arbeit, die wir geleistet haben, um den Aufwand für die Erstellung mehrerer HNSW-Diagramme deutlich zu reduzieren und insbesondere die Kosten für das Zusammenführen von Diagrammen zu senken.
Hintergrund
Um eine überschaubare Anzahl von Segmenten beizubehalten, prüft Lucene regelmäßig, ob Segmente zusammengeführt werden sollen. Dies läuft darauf hinaus, zu prüfen, ob die aktuelle Segmentanzahl eine Zielsegmentanzahl überschreitet, die durch die Basissegmentgröße und die Zusammenführungsrichtlinie bestimmt wird. Wenn die Anzahl überschritten wird, führt Lucene Segmentgruppen zusammen, während die Einschränkung verletzt wird. Dieser Vorgang wurde an anderer Stelle ausführlich beschrieben.
Lucene entscheidet sich für die Zusammenführung ähnlich großer Segmente, da dadurch ein logarithmisches Wachstum der Schreibverstärkung erreicht wird. Im Fall eines Vektorindex ist die Schreibverstärkung die Anzahl der Male, die ein Vektor in ein Diagramm eingefügt wird. Lucene versucht, Segmente in Gruppen von etwa 10 zusammenzuführen. Folglich werden Vektoren in einen Graphen eingefügt, der ungefähr beträgt. mal, wobei die Anzahl der Indexvektoren und die erwartete Anzahl der Basissegmentvektoren ist. Aufgrund des logarithmischen Wachstums liegt die Schreibverstärkung selbst bei großen Indizes im einstelligen Bereich. Die Gesamtzeit, die zum Zusammenführen von Graphen benötigt wird, ist jedoch linear proportional zur Schreibverstärkung.
Beim Zusammenführen von HNSW-Graphen nehmen wir bereits eine kleine Optimierung vor: Wir behalten den Graphen für das größte Segment bei und fügen Vektoren aus den anderen Segmenten darin ein. Dies ist der Grund für den oben genannten 9/10-Faktor. Im Folgenden zeigen wir, wie wir durch die Verwendung von Informationen aus allen Diagrammen, die wir zusammenführen, deutlich bessere Ergebnisse erzielen können.
HNSW-Graphzusammenführung
Bisher haben wir den größten Graphen beibehalten und Vektoren aus den anderen eingefügt, wobei wir die Graphen, die sie enthalten, ignoriert haben. Die zentrale Erkenntnis, die wir im Folgenden nutzen, ist, dass jeder HNSW-Graph, den wir verwerfen, wichtige Näheinformationen über die darin enthaltenen Vektoren enthält. Wir möchten diese Informationen nutzen, um das Einfügen zumindest einiger Vektoren zu beschleunigen.
Wir konzentrieren uns auf das Problem des Einfügens eines kleineren Graphen in einen größeren Graphen , da dies eine atomare Operation ist, die wir zum Erstellen beliebiger Zusammenführungsrichtlinien verwenden können.
Die Strategie besteht darin, eine Teilmenge von Eckpunkten von zu finden, die in den großen Graphen eingefügt werden soll. Wir verwenden dann die Konnektivität dieser Knoten im kleinen Graphen, um das Einfügen der verbleibenden Knoten zu beschleunigen. Im Folgenden verwenden wir und um die Nachbarn eines Knotens im kleinen bzw. großen Graphen zu bezeichnen. Schematisch ist der Ablauf wie folgt.
MERGE-HNSW
Inputs and
1Find to insert into using COMPUTE-JOIN-SET2Insert each vertex into 3for do456FAST-SEARCH-LAYER7SELECT-NEIGHBORS-HEURISTIC8
Wir berechnen die Menge mithilfe eines Verfahrens, das wir unten besprechen (Zeile 1). Dann fügen wir jeden Knoten in mithilfe des Standard-HNSW-Einfügeverfahrens in den großen Graphen ein (Zeile 2). Für jeden Knoten, den wir nicht eingefügt haben, finden wir seine Nachbarn, die wir eingefügt haben, und deren Nachbarn im großen Graphen (Zeilen 4 und 5). Wir verwenden ein mit diesem Set (Zeile 6) gesätes FAST-SEARCH-LAYER -Verfahren, um die Kandidaten für SELECT-NEIGHBORS-HEURISTIC aus dem HNSW- Papier (Zeile 7) zu finden. Tatsächlich ersetzen wir SEARCH-LAYER , um den Kandidatensatz in der Methode INSERT (Algorithmus 1 aus dem Dokument) zu finden, die ansonsten unverändert bleibt. Schließlich fügen wir den Scheitelpunkt hinzu, den wir gerade in eingefügt haben (Zeile 8).
Damit dies funktioniert, ist klar, dass jeder Scheitelpunkt in mindestens einen Nachbarn in haben muss. Tatsächlich verlangen wir, dass für jeden Scheitelpunkt in für ein gewisses , die maximale Schichtkonnektivität, gilt. Wir beobachten, dass in realen HNSW-Diagrammen eine ziemliche Streuung der Scheitelpunktgrade zu sehen ist. Die folgende Abbildung zeigt eine typische kumulative Dichtefunktion des Scheitelpunktgrads für die unterste Ebene eines Lucene HNSW-Diagramms.
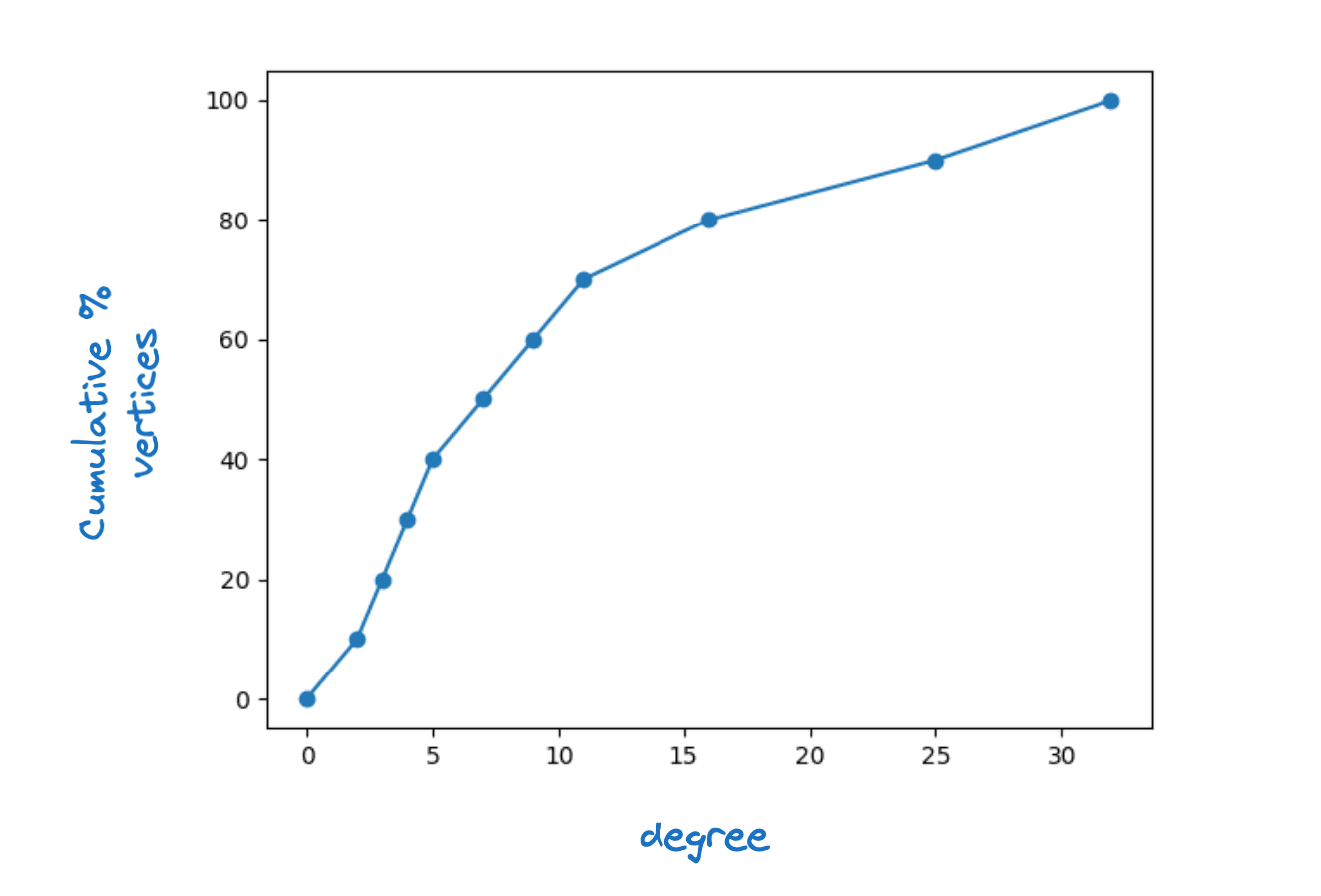
Beispiel für eine Scheitelpunktgradverteilung
Wir haben die Verwendung eines festen Werts für sowie die Möglichkeit untersucht, ihn zu einer Funktion des Scheitelpunktgrads zu machen. Diese zweite Wahl führt zu größeren Beschleunigungen bei minimalen Auswirkungen auf die Grafikqualität, daher habe ich mich für Folgendes entschieden
Beachten Sie, dass | per Definition gleich dem Grad des Scheitelpunkts im kleinen Graphen ist. Eine Untergrenze von zwei bedeutet, dass wir jeden Scheitelpunkt einfügen, dessen Grad kleiner als zwei ist.
Ein einfaches Zählargument legt nahe, dass wir bei sorgfältiger Wahl von nur etwa direkt in einfügen müssen. Konkret färben wir eine Kante des Graphen, wenn wir genau einen ihrer Endknoten in einfügen. Dann wissen wir, dass wir für jeden Knoten in mindestens Kanten einfärben müssen, um mindestens Nachbarn in Darüber hinaus erwarten wir, dass
Dabei ist der durchschnittliche Knotengrad im kleinen Graphen. Für jeden Knoten färben wir höchstens Kanten. Daher beträgt die Gesamtzahl der Kanten, die wir voraussichtlich einfärben werden, höchstens . Wir hoffen, dass wir durch sorgfältige Wahl von annähernd diese Anzahl von Kanten einfärben können. Um alle Eckpunkte abzudecken, muss folgende Bedingung erfüllen:
Dies impliziert, dass .
Vorausgesetzt, SEARCH-LAYER dominiert die Laufzeit, lässt dies darauf schließen, dass wir eine bis zu Beschleunigung der Zusammenführungszeit erreichen könnten. Angesichts des logarithmischen Wachstums der Schreibverstärkung bedeutet dies, dass wir selbst bei sehr großen Indizes die Erstellungszeit im Vergleich zum Erstellen eines Diagramms normalerweise nur verdoppeln würden.
Das Risiko bei dieser Strategie besteht darin, dass wir die Grafikqualität beeinträchtigen. Wir haben es zunächst mit einem No-Op FAST-SEARCH-LAYER versucht. Wir haben festgestellt, dass dies die Qualität des Diagramms in dem Maße verschlechtert, dass die Rückrufrate als Funktion der Latenz beeinträchtigt wird, insbesondere beim Zusammenführen auf ein einzelnes Segment. Anschließend haben wir mithilfe einer eingeschränkten Suche im Diagramm verschiedene Alternativen untersucht. Am Ende war die effektivste Wahl die einfachste. Verwenden Sie SEARCH-LAYER , aber mit einem niedrigen ef_construction. Mit dieser Parametrisierung konnten wir Grafiken von hervorragender Qualität erzielen und die Zusammenführungszeit dennoch durchschnittlich um etwas mehr als 30 % verkürzen.
Berechnung der Join-Menge
Die Suche nach einer guten Join-Menge kann als HNSW-Graphüberdeckungsproblem formuliert werden. Eine Greedy-Heuristik ist eine einfache und effektive Heuristik zur Annäherung an optimale Graphüberdeckungen. Bei unserem Ansatz werden die Knotenpunkte nacheinander in absteigender Reihenfolge der Verstärkung zu hinzugefügt. Der Gewinn ist wie folgt definiert:
Dabei bezeichnet die Anzahl der Nachbarn eines Vektors in und ist die Indikatorfunktion. Der Gewinn beinhaltet die Änderung der Anzahl der Scheitelpunkte, die wir zu hinzugefügt haben, also , da wir unserem Ziel durch das Hinzufügen eines weniger abgedeckten Scheitelpunkts näher kommen. Die Gewinnberechnung wird in der folgenden Abbildung für den zentralen orangefarbenen Scheitelpunkt veranschaulicht.
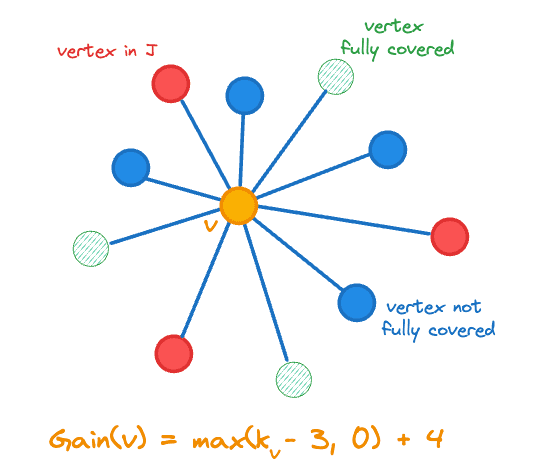
Zum Join-Satz J hinzuzufügender Scheitelpunktgewinn
Wir behalten für jeden Knoten den folgenden Zustand bei:
- Ob es abgestanden ist,
- Sein Gewinn ,
- Die Anzahl der benachbarten Eckpunkte in wird bezeichnet,
- Eine Zufallszahl im Bereich [0,1], die zum Auflösen eines Gleichstands verwendet wird.
Der Pseudocode zum Berechnen des Join-Sets lautet wie folgt.
COMPUTE-JOIN-SET
Inputs
123for do4567while do
8 maximum gain vertex in 9Remove the state for from 10if is not stale then111213for do14mark as stale if 15mark neighbors of stale if
16
17else
18
19if then
20
21return
Wir initialisieren zunächst den Status in den Zeilen 1-5.
In jeder Iteration der Hauptschleife extrahieren wir zunächst den Scheitelpunkt mit der maximalen Verstärkung (Zeile 8) und lösen Gleichstände nach dem Zufallsprinzip auf. Bevor wir Änderungen vornehmen, müssen wir prüfen, ob die Verstärkung des Scheitelpunkts veraltet ist. Insbesondere beeinflussen wir jedes Mal, wenn wir einen Scheitelpunkt zu hinzufügen, den Gewinn anderer Scheitelpunkte:
- Da alle seine Nachbarn einen zusätzlichen Nachbarn in haben, können sich ihre Gewinne ändern (Zeile 14).
- Wenn einer seiner Nachbarn jetzt vollständig gedeckt ist, können sich die Gewinne aller seiner Nachbarn ändern (Zeilen 14-16).
Wir berechnen die Gewinne auf verzögerte Weise neu, d. h. wir berechnen den Gewinn eines Scheitelpunkts nur dann neu, wenn wir ihn in einfügen möchten (Zeilen 18–20). Da die Gewinne immer nur abnehmen, können wir nie einen Scheitelpunkt verpassen, den wir einfügen sollten.
Beachten Sie, dass wir lediglich den Gesamtgewinn der zu hinzugefügten Scheitelpunkte im Auge behalten müssen, um zu bestimmen, wann wir aussteigen müssen. Darüber hinaus wird, obwohl mindestens ein Scheitelpunkt einen von Null verschiedenen Gewinn aufweisen, sodass wir immer Fortschritte machen.
Ergebnisse
Wir haben Experimente mit vier Datensätzen durchgeführt, die zusammen unsere drei unterstützten Distanzmetriken (euklidisch, Kosinus und inneres Produkt) abdecken:
- quora-E5-small: 522931 Dokumente, 384 Dimensionen und verwendet Kosinusähnlichkeit,
- cohere-wikipedia-v2: 1 Million Dokumente, 768 Dimensionen und verwendet Kosinusähnlichkeit,
- Kern: 1 Million Dokumente, 960 Dimensionen und verwendet euklidische Distanz und
- cohere-wikipedia-v3: 1 Mio. Dokumente, 1024 Dimensionen und verwendet das maximale innere Produkt.
Für jeden Datensatz bewerten wir zwei Quantisierungsstufen:
- int8 – verwendet eine 1-Byte-Ganzzahl pro Dimension und
- BBQ – das ein einzelnes Bit pro Dimension verwendet.
Schließlich haben wir für jedes Experiment die Suchqualität bei zwei Abruftiefen bewertet und nach dem Erstellen des Index und anschließend nach der erzwungenen Zusammenführung zu einem einzelnen Segment untersucht.
Zusammenfassend lässt sich sagen, dass wir durchgängig erhebliche Beschleunigungen bei der Indizierung und Zusammenführung erzielen und dabei in allen Fällen die Grafikqualität und damit die Suchleistung beibehalten.
Experiment 1: int8-Quantisierung
Die durchschnittlichen Beschleunigungen von der Basislinie bis zum Kandidaten, die vorgeschlagenen Änderungen, sind:
Beschleunigung der Indexzeit: 1,28
Beschleunigung der Force Merge: 1,72
Dies entspricht folgender Laufzeitaufteilung
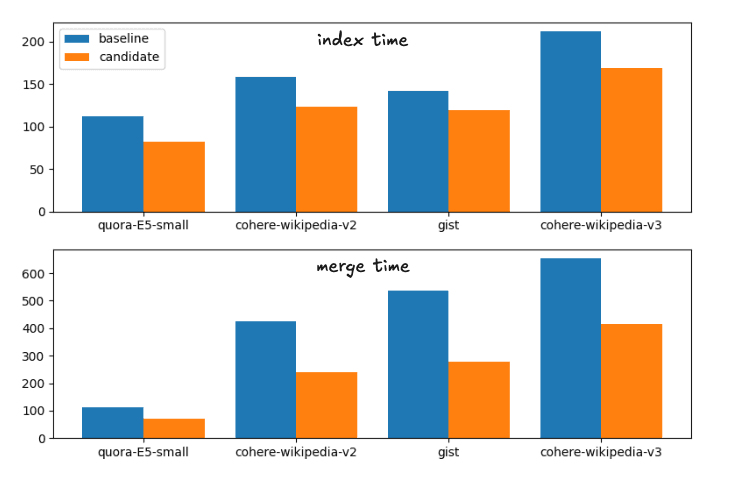
Index- und Zusammenführungszeiten für die Baseline- und Kandidatenzusammenführungsstrategien
Der Vollständigkeit halber sind die genauen Zeiten
| Index | Verschmelzen | |||
|---|---|---|---|---|
| Datensatz | Basislinie | Kandidat | Entwickeln | Kandidat |
| Quora-E5-klein | 112,41 s | 81,55 s | 113,81 s | 70,87 s |
| wiki-cohere-v2 | 158,1 s | 122,95 s | 425,20 s | 239,28 s |
| Kern | 141,82 s | 119,26 s | 536,07 s | 279,05 s |
| wiki-cohere-v3 | 211,86 s | 168,22 s | 654,97 s | 414,12 s |
Unten zeigen wir die Diagramme „Rückruf vs. Latenz“, die den Kandidaten (gestrichelte Linien) mit der Basislinie bei zwei Abruftiefen vergleichen: Rückruf@10 und Rückruf@100 für Indizes mit mehreren Segmenten (das Endergebnis unserer Standard-Zusammenführungsstrategie nach der Indizierung aller Vektoren) und nach der erzwungenen Zusammenführung zu einem einzelnen Segment. Eine Kurve, die höher und weiter links liegt, ist besser, da sie eine höhere Rückrufrate bei geringerer Latenz bedeutet.
Wie Sie sehen, ist der Kandidat für mehrere Segmentindizes für den Cohere v3-Datensatz besser und für alle anderen Datensätze etwas schlechter, aber fast vergleichbar. Nach der Zusammenführung zu einem einzigen Segment sind die Erinnerungskurven in allen Fällen nahezu identisch.
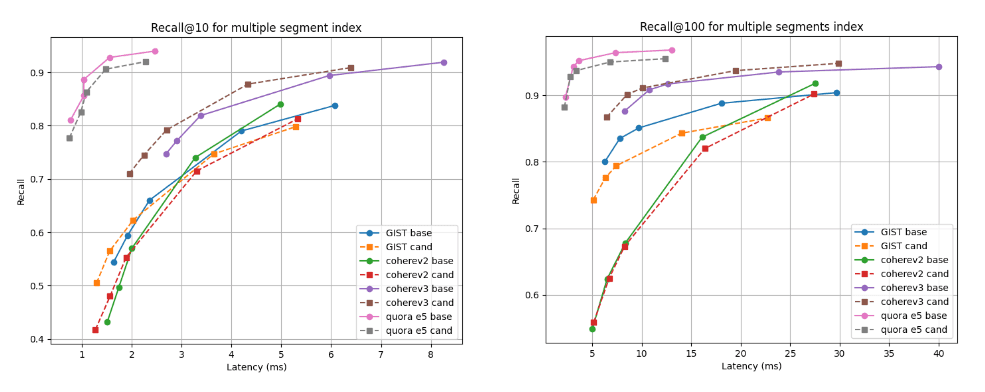
Rückruf @10 und @100 im Vergleich zur Latenz nach dem Erstellen des Index
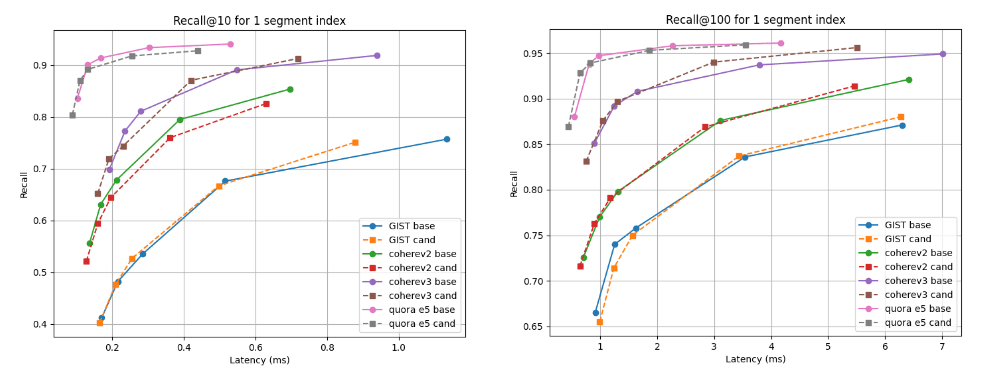
Rückruf @10 und @100 im Vergleich zur Latenz nach der Zusammenführung zu einem einzelnen Segment
Experiment 2: BBQ-Quantisierung
Die durchschnittlichen Beschleunigungen von der Basislinie zum Kandidaten sind:
Beschleunigung der Indexzeit: 1,33
Beschleunigung der Force Merge: 1,34
Dies entspricht folgender Laufzeitaufteilung
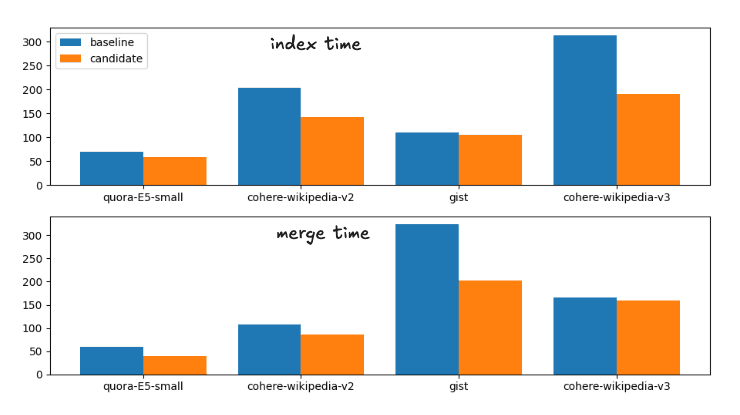
Index- und Zusammenführungszeit für die Baseline- und Kandidatenzusammenführungsstrategien
Der Vollständigkeit halber sind die genauen Zeiten
| Index | Verschmelzen | |||
|---|---|---|---|---|
| Datensatz | Basislinie | Kandidat | Entwickeln | Kandidat |
| Quora-E5-klein | 70,71 s | 58,25 s | 59,38 s | 40,15 s |
| wiki-cohere-v2 | 203,08 s | 142,27 s | 107,27 s | 85,68 s |
| Kern | 110,35 s | 105,52 s | 323,66 s | 202,2 s |
| wiki-cohere-v3 | 313,43 s | 190,63 s | 165,98 s | 159,95 s |
Bei Indizes mit mehreren Segmenten ist der Kandidat für fast alle Datensätze besser, mit Ausnahme von Cohere v2, wo die Basislinie etwas besser ist. Für die einzelnen Segmentindizes sind die Recall-Kurven in allen Fällen nahezu identisch.
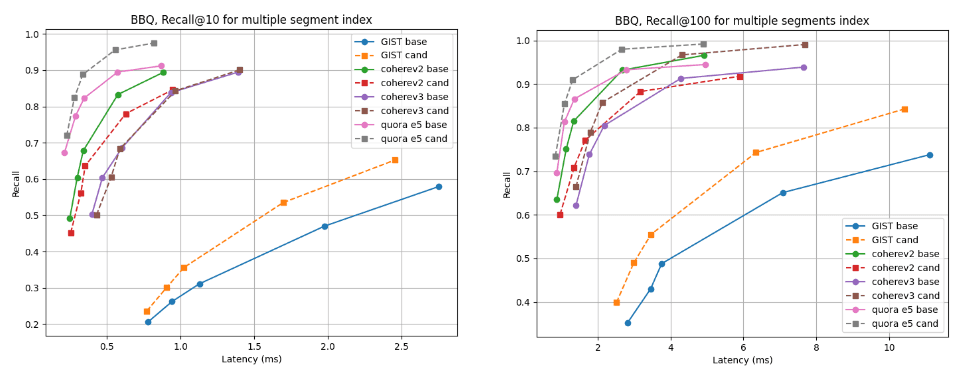
Rückruf @10 und @100 im Vergleich zur Latenz nach dem Erstellen des Index
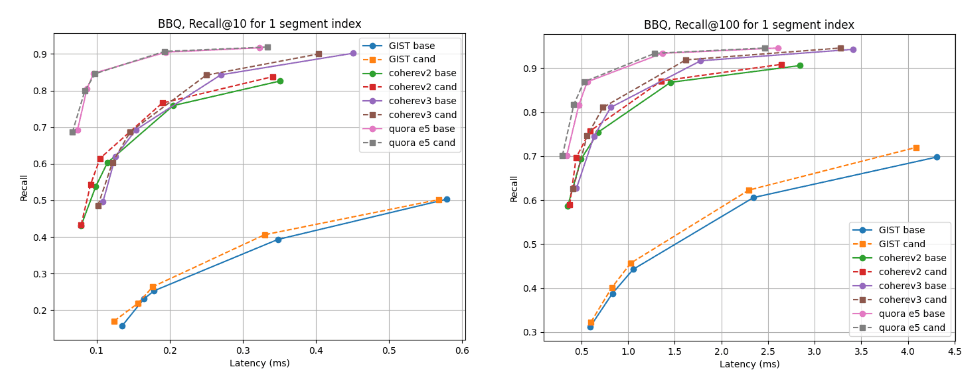
Erinnern Sie sich an @10 und @100 im Vergleich zur Latenz nach der Zusammenführung zu einem einzigen Segment
Fazit
Der in diesem Blog besprochene Algorithmus wird im kommenden Lucene 10.2 und in der darauf basierenden Elasticsearch-Version verfügbar sein. Benutzer können in diesen neuen Versionen von der verbesserten Zusammenführungsleistung und der verkürzten Indexerstellungszeit profitieren. Diese Änderung ist Teil unserer kontinuierlichen Bemühungen, Lucene und Elasticsearch für die Vektor- und Hybridsuche schnell und effizient zu machen.




