De la recherche vectorielle aux puissantes API REST, Elasticsearch offre aux développeurs la boîte à outils de recherche la plus complète. Explorez nos notebooks d’exemples sur GitHub pour tester de nouveaux cas d’usage. Vous pouvez également démarrer votre essai gratuit ou exécuter Elasticsearch en local dès aujourd’hui.
Dans le passé, nous avons abordé certains des défis posés par la recherche dans plusieurs graphes de HNSW et la manière dont nous avons pu les atténuer. À cette occasion, nous avons fait allusion à d'autres améliorations que nous avions prévues. Ce billet est l'aboutissement de ce travail.
Vous vous demandez peut-être pourquoi utiliser des graphiques multiples ? Il s'agit d'un effet secondaire d'un choix architectural de Lucene : les segments immuables. Comme pour la plupart des choix architecturaux, il y a des avantages et des inconvénients. Par exemple, nous avons récemment obtenu la certification Serverless Elasticsearch. Dans ce contexte, nous avons tiré des avantages très importants des segments immuables, notamment une réplication efficace de l'index et la possibilité de découpler le calcul de l'index et de la requête et de les faire évoluer indépendamment. Pour la quantification vectorielle, les fusions de segments nous donnent la possibilité de mettre à jour les paramètres pour les adapter aux caractéristiques des données. Dans le même ordre d'idées, nous pensons que la possibilité de mesurer les caractéristiques des données et de revoir les choix d'indexation présente d'autres avantages.
Dans ce billet, nous discuterons du travail que nous avons effectué pour réduire de manière significative la charge de travail liée à la construction de plusieurs graphes HNSW et, en particulier, pour réduire le coût de la fusion des graphes.
Arrière-plan
Afin de maintenir un nombre raisonnable de segments, Lucene vérifie périodiquement s'il doit fusionner des segments. Cela revient à vérifier si le nombre de segments actuel dépasse un nombre de segments cible, qui est déterminé par la taille du segment de base et la politique de fusion. Si le nombre est dépassé, Lucene fusionne les groupes de segments alors que la contrainte n'est pas respectée. Ce processus a été décrit en détail dans d'autres documents.
Lucene choisit de fusionner des segments de taille similaire car cela permet d'obtenir une croissance logarithmique de l'amplification de l'écriture. Dans le cas d'un index vectoriel, l'amplification de l'écriture est le nombre de fois qu'un vecteur sera inséré dans un graphique. Lucene essaiera de fusionner les segments par groupes d'environ 10. Par conséquent, les vecteurs sont insérés dans un graphe environ 1+\frac{9}{10}\log_{10}\left (\frac{n}{n_0}\right ) fois, où le nombre de vecteurs de l'index et est le nombre de vecteurs du segment de base attendu. En raison de la croissance logarithmique, l'amplification de l'écriture est à un chiffre, même pour les indices les plus importants. Cependant, le temps total passé à fusionner les graphes est linéairement proportionnel à l'amplification de l'écriture.
Lors de la fusion des graphes HNSW, nous procédons déjà à une petite optimisation : nous conservons le graphe du plus grand segment et y insérons les vecteurs des autres segments. C'est la raison pour laquelle le facteur 9/10 est mentionné ci-dessus. Nous montrons ci-dessous comment nous pouvons faire beaucoup mieux en utilisant les informations de tous les graphiques que nous fusionnons.
Fusion du graphique HNSW
Auparavant, nous retenions le plus grand graphe et insérions des vecteurs provenant des autres en ignorant les graphes qui les contiennent. L'idée clé que nous utilisons ci-dessous est que chaque graphe HNSW que nous écartons contient des informations de proximité importantes sur les vecteurs qu'il contient. Nous aimerions utiliser cette information pour accélérer l'insertion d'au moins une partie des vecteurs.
Nous nous concentrons sur le problème de l'insertion d'un petit graphe dans un graphe plus grand , puisqu'il s'agit d'une opération atomique que nous pouvons utiliser pour construire n'importe quelle politique de fusion.
La stratégie consiste à trouver un sous-ensemble de sommets de l' à insérer dans le grand graphe. Nous utilisons ensuite la connectivité de ces sommets dans le petit graphe pour accélérer l'insertion des sommets restants Dans ce qui suit, nous utilisons et pour désigner les voisins d'un sommet dans le petit et le grand graphe, respectivement. Schématiquement, le processus est le suivant.
MERGE-HNSW
Inputs and
1Find to insert into using COMPUTE-JOIN-SET2Insert each vertex into 3for do456FAST-SEARCH-LAYER7SELECT-NEIGHBORS-HEURISTIC8
Nous calculons l'ensemble à l'aide d'une procédure que nous décrivons ci-dessous (ligne 1). Ensuite, nous insérons chaque sommet de dans le grand graphe à l'aide de la procédure d'insertion HNSW standard (ligne 2). Pour chaque sommet que nous n'avons pas inséré, nous trouvons ses voisins que nous avons insérés et leurs voisins dans le grand graphe (lignes 4 et 5). Nous utilisons une procédure FAST-SEARCH-LAYER avec cet ensemble (ligne 6) pour trouver les candidats pour le site SELECT-NEIGHBORS-HEURISTIC de l'article HNSW (ligne 7). En fait, nous remplaçons SEARCH-LAYER pour trouver l'ensemble de candidats dans la méthode INSERT (Algorithme 1 de l'article), qui est par ailleurs inchangée. Enfin, nous ajoutons le sommet que nous venons d'insérer dans (ligne 8).
Il est clair que pour que cela fonctionne, chaque sommet dans doit avoir au moins un voisin dans En fait, nous exigeons que pour chaque sommet dans que pour quelque M, la connectivité maximale de la couche. Nous observons que dans les graphes HNSW réels, les degrés des sommets sont assez variés. La figure ci-dessous montre une fonction de densité cumulative typique du degré de sommet pour la couche inférieure d'un graphique Lucene HNSW.
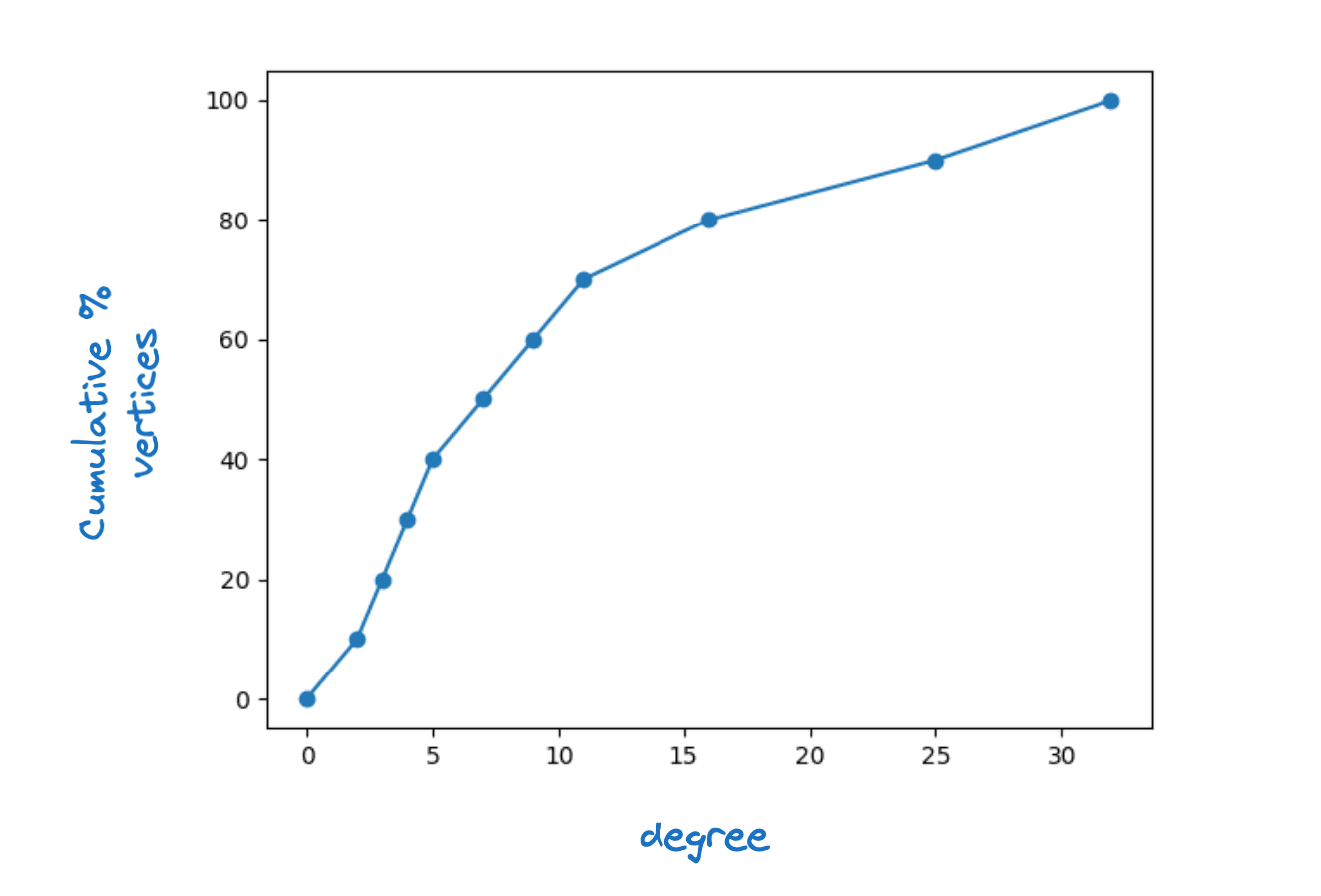
Exemple de distribution des degrés des sommets
Nous avons étudié la possibilité d'utiliser une valeur fixe pour et de la faire dépendre du degré du sommet. Ce deuxième choix conduit à des accélérations plus importantes avec un impact minimal sur la qualité du graphe, nous avons donc opté pour ce qui suit
Notez que | est égal au degré du sommet dans le petit graphe par définition. Le fait d'avoir une limite inférieure de deux signifie que nous insérerons tous les sommets dont le degré est inférieur à deux.
Un simple argument de comptage suggère que si nous choisissons avec soin, il nous suffit d'insérer directement dans Plus précisément, nous colorons une arête du graphe si nous insérons exactement l'un de ses sommets d'extrémité dans Nous savons alors que pour que chaque sommet de ait au moins voisins dans , nous devons colorer au moins \sum_ arêtes. En outre, nous nous attendons à ce que
Ici, \mathbb {E}_U\left [N_s(U)|\right] est le degré moyen des sommets dans le petit graphe. Pour chaque sommet , nous colorons au plus arêtes. Par conséquent, le nombre total d'arêtes que nous prévoyons de colorer est au maximum de _U\left [|N_s(U)|\right]. Nous espérons qu'en choisissant avec soin, nous colorerons un nombre d'arêtes proche de ce nombre et donc, pour couvrir tous les sommets, doit satisfaire à
Ceci implique que |J|=\frac{1}{4}(|V_s|-|J|)=\frac{4}{5}\frac {1}{4}|V_s|=\frac{1}{5}|V_s|.
Si SEARCH-LAYER domine le temps d'exécution, cela signifie que nous pourrions accélérer le temps de fusion jusqu'à Compte tenu de la croissance logarithmique de l'amplification de l'écriture, cela signifie que même pour de très grands indices, nous ne ferions que doubler le temps de construction par rapport à la construction d'un seul graphique.
Le risque de cette stratégie est de nuire à la qualité du graphique. Nous avons d'abord essayé avec une version sans option FAST-SEARCH-LAYER. Nous avons constaté que cela dégradait la qualité des graphes dans la mesure où le rappel en fonction de la latence était affecté, en particulier lors de la fusion en un seul segment. Nous avons ensuite exploré diverses alternatives en effectuant une recherche limitée dans le graphique. Finalement, le choix le plus efficace a été le plus simple. Utilisez SEARCH-LAYER mais avec une faible ef_construction. Ce paramétrage nous a permis d'obtenir des graphes d'excellente qualité tout en réduisant le temps de fusion d'un peu plus de 30% en moyenne.
Calcul de l'ensemble de jonction
La recherche d'un bon ensemble de jointures peut être formulée comme un problème de couverture de graphe HNSW. Une heuristique gourmande est une heuristique simple et efficace pour approximer les couvertures optimales des graphes. L'approche que nous adoptons consiste à sélectionner les sommets un par un pour les ajouter à dans l'ordre décroissant des gains. Le gain est défini comme suit :
Ici, représente le nombre de voisins d'un vecteur dans et est la fonction indicatrice. Le gain comprend la variation du nombre de sommets que nous avons ajoutés à , c'est-à-dire \max , puisque nous nous rapprochons de notre objectif en ajoutant un sommet moins couvert. Le calcul du gain est illustré dans la figure ci-dessous pour le sommet central orange.
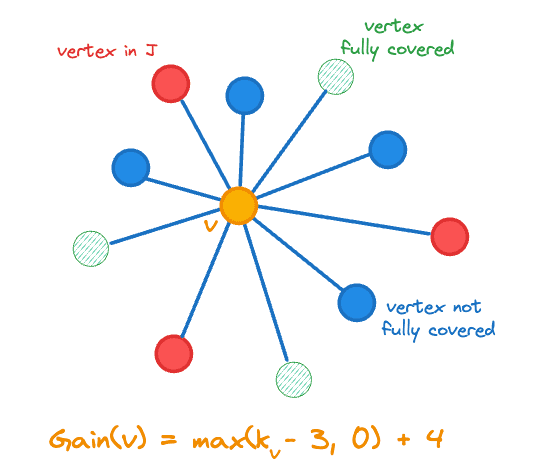
Gain de sommet à ajouter à l'ensemble de jointure J
Nous conservons l'état suivant pour chaque sommet
- S'il est périmé,
- Son gain ,
- Le nombre de sommets adjacents dans est noté
- Un nombre aléatoire dans l'intervalle [0,1] qui est utilisé pour départager les ex-aequo.
Le pseudo-code pour le calcul de l'ensemble de jonction est le suivant.
COMPUTE-JOIN-SET
Inputs
123for do4567while do
8 maximum gain vertex in 9Remove the state for from 10if is not stale then111213for do14mark as stale if 15mark neighbors of stale if
16
17else
18
19if then
20
21return
Nous commençons par initialiser l'état dans les lignes 1 à 5.
À chaque itération de la boucle principale, nous extrayons d'abord le sommet de gain maximal (ligne 8), en brisant les égalités de manière aléatoire. Avant de procéder à toute modification, nous devons vérifier si le gain du sommet est périmé. En particulier, chaque fois que nous ajoutons un sommet à , nous affectons le gain d'autres sommets :
- Puisque tous ses voisins ont un voisin supplémentaire en , leurs gains peuvent changer (ligne 14)
- Si l'un de ses voisins est maintenant entièrement couvert, tous les gains de ses voisins peuvent changer (lignes 14-16).
Nous recalculons les gains paresseusement, c'est-à-dire que nous ne recalculons le gain d'un sommet que si nous voulons l'insérer dans (lignes 18-20). Puisque les gains ne font que diminuer, nous ne pouvons jamais manquer un sommet que nous devrions insérer.
Notez que nous avons simplement besoin de suivre le gain total de sommets que nous avons ajoutés à pour déterminer quand sortir. En outre, pendant que Gain_{tot}< Gain_ {exit}au moins un sommet aura un gain non nul, de sorte que nous progressons toujours.
Résultats
Nous avons mené des expériences sur quatre ensembles de données qui, ensemble, couvrent les trois mesures de distance prises en charge (Euclidean, cosinus et produit intérieur) :
- quora-E5-small : 522931 documents, 384 dimensions et utilise la similarité cosinus,
- cohere-wikipedia-v2 : 1M documents, 768 dimensions et utilise la similarité cosinus,
- gist : 1M documents, 960 dimensions et utilise la distance euclidienne, et
- cohere-wikipedia-v3 : 1M documents, 1024 dimensions et utilise le produit intérieur maximum.
Pour chaque ensemble de données, nous évaluons deux niveaux de quantification :
- int8 - qui utilise un entier de 1 octet par dimension et
- BBQ - qui utilise un seul bit par dimension.
Enfin, pour chaque expérience, nous avons évalué la qualité de la recherche à deux profondeurs d'extraction et nous l'avons examinée après la construction de l'index, puis après la fusion forcée en un seul segment.
En résumé, nous obtenons des accélérations substantielles et constantes dans l'indexation et la fusion tout en maintenant la qualité du graphe et donc les performances de recherche dans tous les cas.
Expérience 1 : quantification int8
Les gains de vitesse moyens entre la ligne de base et le candidat, les changements proposés, sont les suivants :
Accélération du temps d'indexation : 1,fois
Accélération de la fusion forcée : 1,fois
Cela correspond à la répartition suivante des durées d'exécution
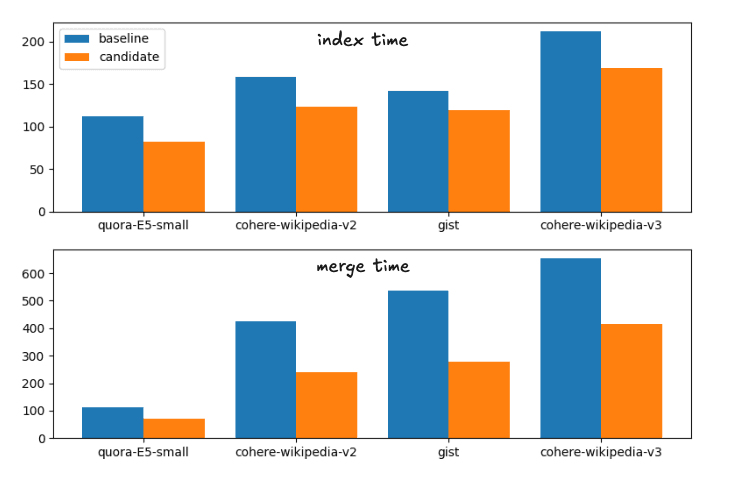
Temps d'indexation et de fusion pour la stratégie de fusion de base et la stratégie de fusion candidate
Par souci d'exhaustivité, les horaires exacts sont les suivants
| Index | Fusionner | |||
|---|---|---|---|---|
| Ensemble de données | ligne de base | candidat | Développer | candidat |
| quora-E5-petit | 112.41s | 81.55s | 113.81s | 70.87s |
| wiki-cohere-v2 | 158.1s | 122.95s | 425.20s | 239.28s |
| liste | 141.82s | 119.26s | 536.07s | 279.05s |
| wiki-cohere-v3 | 211.86s | 168.22s | 654.97s | 414.12s |
Nous présentons ci-dessous les graphiques de rappel et de latence qui comparent le candidat (lignes pointillées) à la ligne de base à deux profondeurs de recherche : rappel@10 et rappel@100 pour les index avec plusieurs segments (le résultat final de notre stratégie de fusion par défaut après l'indexation de tous les vecteurs) et après la fusion forcée à un seul segment. Une courbe plus haute et plus à gauche est meilleure, ce qui signifie une meilleure mémorisation avec une latence plus faible.
Comme vous pouvez le constater, pour les indices de segments multiples, le candidat est meilleur pour l'ensemble de données Cohere v3 et légèrement moins bon, mais presque comparable, pour tous les autres ensembles de données. Après la fusion en un seul segment, les courbes de rappel sont presque identiques dans tous les cas.
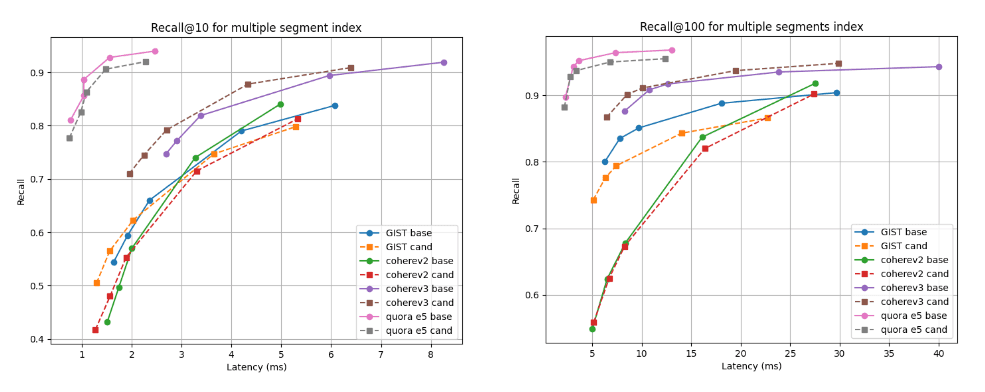
Rappel @10 et @100 vs latence après construction de l'index
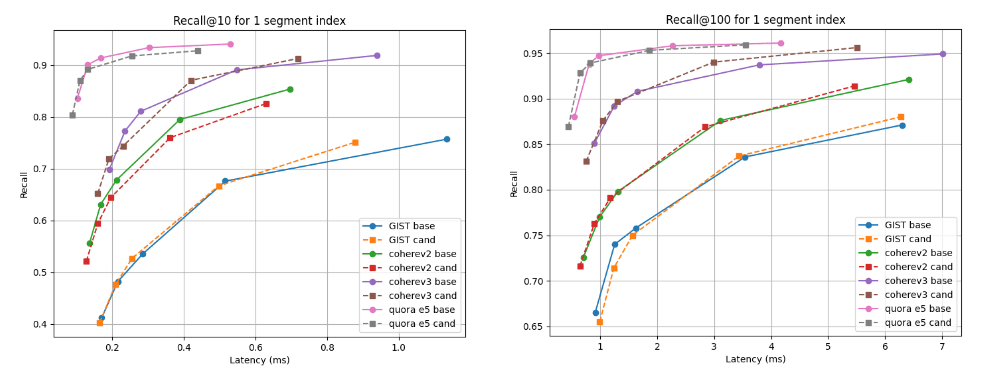
Rappel @10 et @100 vs latence après fusion en un seul segment
Expérience 2 : Quantification BBQ
Les gains de vitesse moyens entre la ligne de base et le candidat sont les suivants :
Accélération du temps d'indexation : 1,fois
Accélération de la fusion forcée : 1,fois
Cela correspond à la répartition suivante des durées d'exécution
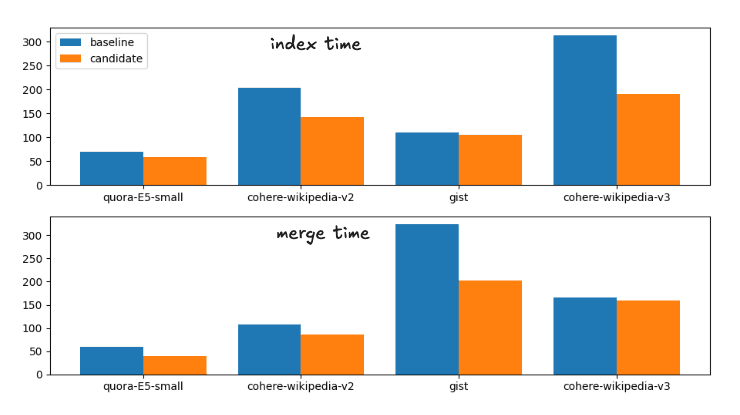
Temps d'indexation et de fusion pour la stratégie de fusion de base et la stratégie de fusion candidate
Par souci d'exhaustivité, les horaires exacts sont les suivants
| Index | Fusionner | |||
|---|---|---|---|---|
| Ensemble de données | ligne de base | candidat | Développer | candidat |
| quora-E5-petit | 70.71s | 58.25s | 59.38s | 40.15s |
| wiki-cohere-v2 | 203.08s | 142.27s | 107.27s | 85.68s |
| liste | 110.35s | 105.52s | 323.66s | 202.2s |
| wiki-cohere-v3 | 313.43s | 190.63s | 165.98s | 159.95s |
Pour les indices de segments multiples, le candidat est meilleur pour presque tous les ensembles de données, à l'exception de cohere v2 où la ligne de base est légèrement meilleure. Pour les indices de segment unique, les courbes de rappel sont presque identiques dans tous les cas.
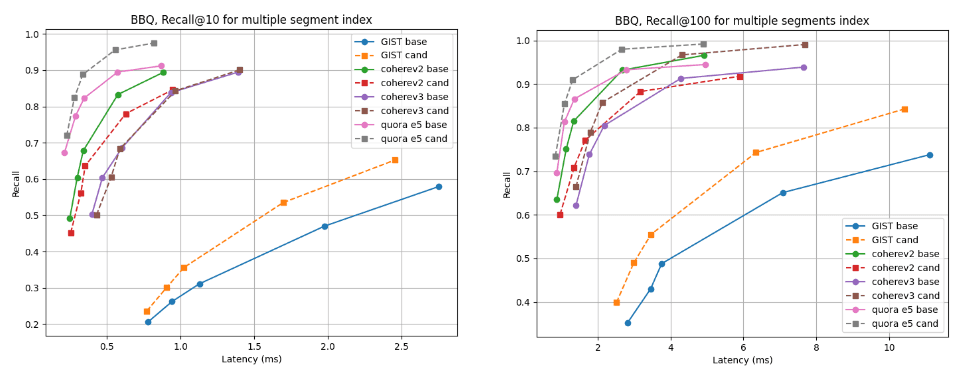
Rappel @10 et @100 vs latence après construction de l'index
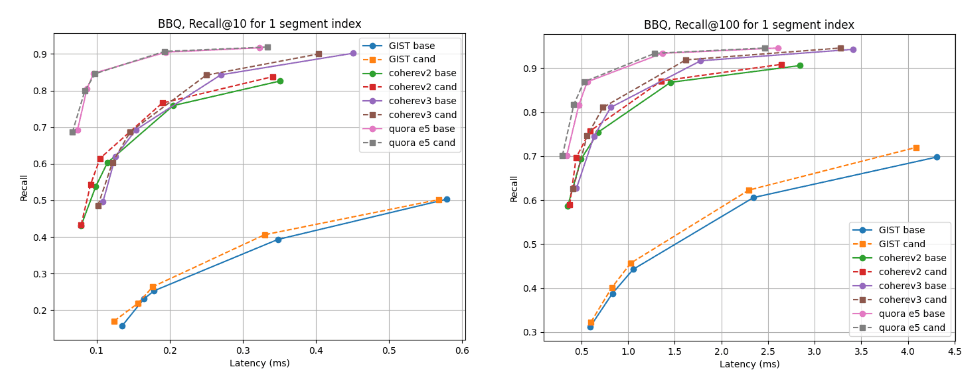
Rappel @10 et @100 vs latence après fusion en un seul segment
Conclusion
L'algorithme présenté dans ce blog sera disponible dans la prochaine version de Lucene 10.2, ainsi que dans la version d'Elasticsearch qui est basée sur cette dernière. Les utilisateurs pourront profiter de l'amélioration des performances de fusion et de la réduction du temps de construction de l'index dans ces nouvelles versions. Ce changement fait partie de nos efforts continus pour rendre Lucene et Elasticsearch rapides et efficaces pour la recherche vectorielle et hybride.




