ベクトル検索から強力なREST APIまで、Elasticsearchは開発者に最も広範な検索ツールキットを提供します。GitHubのサンプルノートブックにアクセスして新しいことを試してみましょう。また、無料トライアルを始めるか、ローカルでElasticsearchを実行することもできます。
以前、複数の HNSW グラフを 検索する必要がある場合に生じるいくつかの課題と、その課題をどのように軽減できるか について説明しました 。当時、私たちは計画していたさらなる改善点についても触れました。この投稿はその作業の集大成です。
なぜ複数のグラフを使用するのかと疑問に思うかもしれません。これは、Lucene のアーキテクチャ上の選択である不変セグメントによる副作用です。ほとんどのアーキテクチャ上の選択と同様に、長所と短所があります。たとえば、最近 Serverless Elasticsearch が GA になりました。この文脈において、私たちは不変セグメントから、効率的なインデックス レプリケーションや、インデックスとクエリの計算を分離して個別に自動スケーリングする機能など、非常に大きなメリットを得ています。ベクトル量子化の場合、セグメントのマージにより、パラメータを更新してデータ特性に適合させることができます。これに沿って、データ特性を測定し、インデックスの選択を再検討する機会を持つことで得られる他の利点もあると考えています。
この投稿では、複数の HNSW グラフを構築する際のオーバーヘッドを大幅に削減し、特にグラフのマージにかかるコストを削減するために私たちが行ってきた作業について説明します。
背景
管理可能な数のセグメントを維持するために、Lucene はセグメントをマージする必要があるかどうかを定期的に確認します。これは、現在のセグメント数が、基本セグメント サイズとマージ ポリシーによって決定されるターゲット セグメント数を超えているかどうかを確認することになります。カウントを超過すると、Lucene は制約に違反しながらセグメントのグループを結合します。このプロセスについては他の場所で詳しく説明されています。
Lucene は、書き込み増幅の対数的増加を実現するため、同様のサイズのセグメントを結合することを選択します。ベクトル インデックスの場合、書き込み増幅はベクトルがグラフに挿入される回数です。Luceneはセグメントを約10個のグループにまとめ、マージしようとします。その結果、ベクトルはグラフに約挿入されます。 ここで、 はインデックス ベクトル数、 予想される基本セグメント ベクトル数です。対数増加のため、巨大なインデックスの場合でも書き込み増幅は 1 桁になります。ただし、グラフのマージに費やされる合計時間は、書き込み増幅に直線的に比例します。
HNSW グラフをマージする際には、最大セグメントのグラフを保持し、他のセグメントのベクトルをそのグラフに挿入するという、小さな最適化をすでに行っています。これが上記の 9/10 要因の理由です。以下では、マージするすべてのグラフの情報を使用することで、どのように大幅に改善できるかを示します。
HNSW グラフのマージ
これまでは、最大のグラフを保持し、他のグラフからベクトルを挿入し、それらを含むグラフは無視していました。以下で利用する重要な洞察は、破棄する各 HNSW グラフには、それに含まれるベクトルに関する重要な近接情報が含まれているということです。この情報を使用して、少なくとも一部のベクトルの挿入を高速化したいと考えています。
これは任意のマージポリシーを構築するために使用できるアトミック操作であるため、小さなグラフを大きなグラフに挿入する問題に焦点を当てます。
戦略は、 の頂点のサブセットを見つけて、大きなグラフに挿入することです。次に、小さなグラフ内のこれらの頂点の接続性を使用して、残りの頂点の挿入を高速化します。以下では、小さいグラフと大きいグラフの頂点 の隣接点をそれぞれ と で表します。図式的にプロセスは次のとおりです。
MERGE-HNSW
Inputs and
1Find to insert into using COMPUTE-JOIN-SET2Insert each vertex into 3for do456FAST-SEARCH-LAYER7SELECT-NEIGHBORS-HEURISTIC8
以下で説明する手順 (1 行目) を使用して、セットを計算します。次に、標準の HNSW 挿入手順 (2 行目) を使用して、 内のすべての頂点を大きなグラフに挿入します。挿入していない各頂点については、挿入した隣接頂点と、大きなグラフ内でのその隣接頂点を見つけます (4 行目と 5 行目)。このセットでシードされたFAST-SEARCH-LAYER手順 (6 行目) を使用して、HNSW論文からSELECT-NEIGHBORS-HEURISTICの候補を検索します (7 行目)。実際には、 SEARCH-LAYER INSERTメソッド (論文のアルゴリズム 1) の候補セットを見つけるために置き換えていますが、それ以外は変更されていません。最後に、先ほど挿入した頂点を (行 8) に追加します。
これが機能するためには、 内のすべての頂点が内に少なくとも 1 つの隣接頂点を持つ必要があることは明らかです。実際、 内のすべての頂点に対して、 (あるに対して) が最大のレイヤー接続性であることが必要です。実際の HNSW グラフでは、頂点次数がかなり広がっていることがわかります。下の図は、Lucene HNSW グラフの最下層の頂点次数の典型的な累積密度関数を示しています。
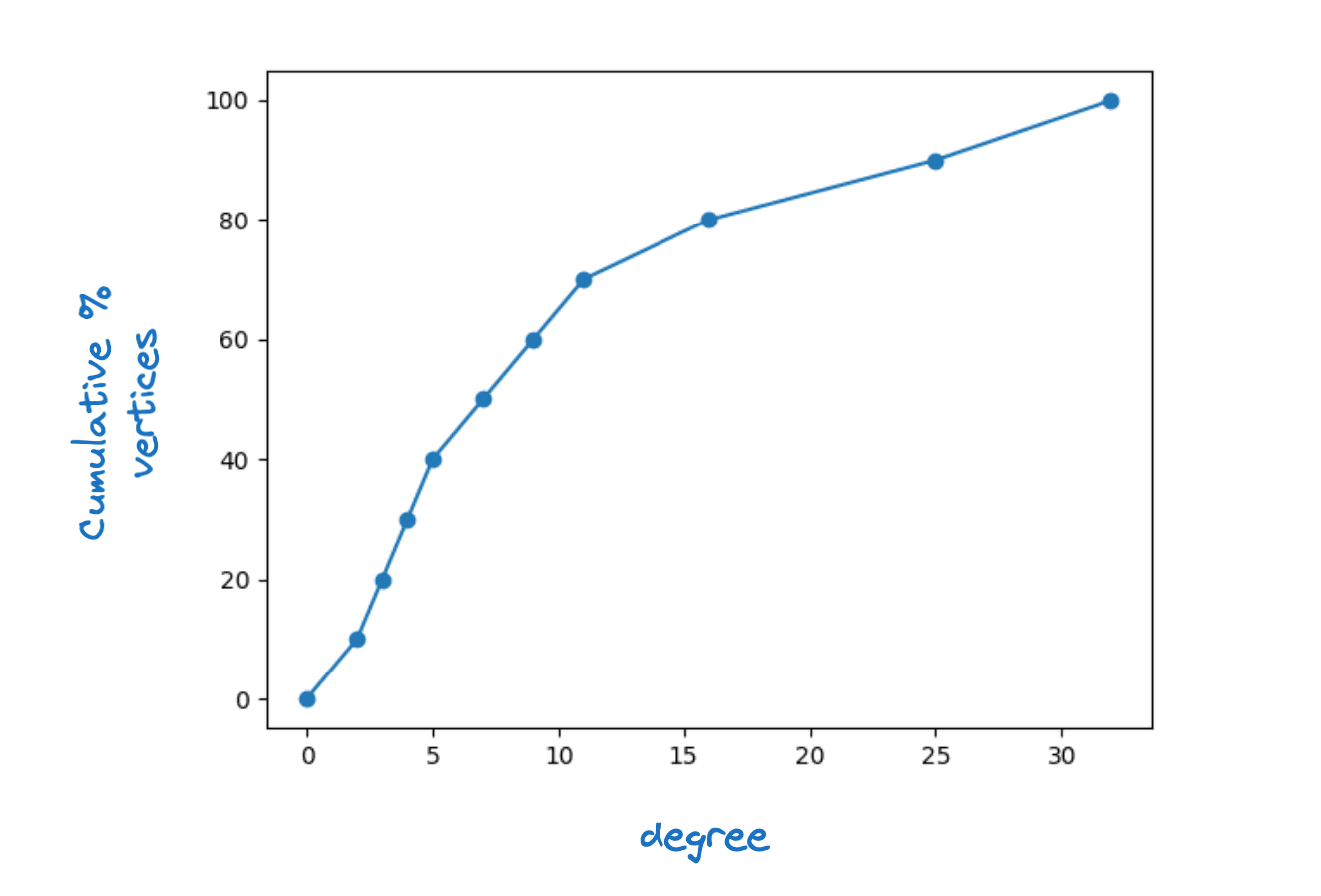
頂点次数分布の例
に固定値を使用することと、それを頂点次数の関数にすることを検討しました。この2番目の選択肢は、グラフの品質への影響を最小限に抑えながら大幅なスピードアップにつながるため、次の方法を採用しました。
定義により、 | は小さなグラフの頂点の次数に等しいことに注意してください。下限が 2 の場合、次数が 2 未満のすべての頂点が挿入されます。
単純な計算の議論によれば、 慎重に選択すれば、約に直接挿入するだけでよいことがわかります。具体的には、グラフの端の頂点の 1 つをに挿入すると、グラフのエッジに色を付けます。すると、 内に少なくとも 個の 隣接頂点を持つためには、少なくとも 個の 辺を色付けする必要があることがわかります。さらに、我々は
ここで、 小さなグラフ内の平均頂点次数です。J内の各頂点に対して、最大での辺を色付けします。したがって、色付けすると予想されるエッジの総数は最大でとなります。慎重に選択することで、この辺の数に近い色を塗ることができると期待しており、すべての頂点をカバーするには満たす必要がある。
これは、 を意味します。
SEARCH-LAYERが実行時間を支配すると、マージ時間を最大高速化できる可能性があります。書き込み増幅の対数的増加を考慮すると、非常に大きなインデックスの場合でも、通常は 1 つのグラフを構築する場合と比べて構築時間が 2 倍になるだけです。
この戦略のリスクは、グラフの品質が損なわれることです。最初は何も実行しないFAST-SEARCH-LAYERを試しました。これにより、特に単一のセグメントにマージするときに、レイテンシの関数としてのリコールが影響を受ける程度にグラフの品質が低下することがわかりました。次に、グラフの限定的な検索を使用して、さまざまな代替案を検討しました。結局、最も効果的な選択は最も単純なものでした。SEARCH-LAYERを使用しますが、 ef_constructionは低くします。このパラメータ化により、優れた品質のグラフを実現しながらも、マージ時間を平均で 30% 強短縮することができました。
結合セットの計算
適切な結合セットを見つけることは、HNSW グラフ カバー問題として定式化できます。貪欲ヒューリスティックは、最適なグラフカバーを近似するためのシンプルで効果的なヒューリスティックです。私たちが採用するアプローチでは、ゲインが減少する順に頂点を 1 つずつ選択してに追加します。ゲインは次のように定義されます。
ここで、 におけるベクトル の近傍の数を表し、 は 指示関数である。ゲインには、 に追加した頂点の数の変化、つまりが含まれます。これは、カバーされていない頂点を追加することで目標に近づくためです。中央のオレンジ色の頂点のゲイン計算を下の図に示します。
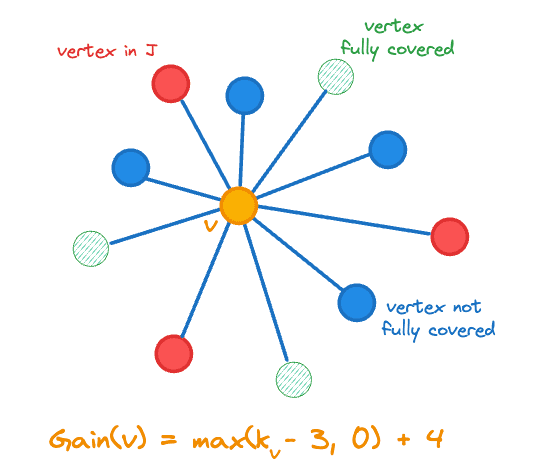
結合セット J に追加する頂点ゲイン
各頂点に対して次の状態を維持します。
- 古くなっても、
- そのゲイン 、
- 内の隣接頂点の数はと表され、
- タイブレークに使用される範囲 [0,1] 内の乱数。
結合セットを計算するための疑似コードは次のとおりです。
COMPUTE-JOIN-SET
Inputs
123for do4567while do
8 maximum gain vertex in 9Remove the state for from 10if is not stale then111213for do14mark as stale if 15mark neighbors of stale if
16
17else
18
19if then
20
21return
まず 1 行目から 5 行目で状態を初期化します。
メイン ループの各反復では、最初に最大ゲイン頂点 (行 8) を抽出し、同点の場合はランダムに決定します。変更を加える前に、頂点のゲインが古くなっているかどうかを確認する必要があります。特に、 に頂点を追加するたびに、他の頂点のゲインに影響を与えます。
- すべての隣接ノードはに追加の隣接ノードを持つため、ゲインは変化する可能性がある(14行目)
- いずれかの隣接セルが完全にカバーされている場合、その隣接セルのゲインはすべて変化する可能性があります(14~16行目)
ゲインは遅延方式で再計算されるため、頂点をに挿入する場合にのみ、その頂点のゲインを再計算します (18 ~ 20 行目)。ゲインは常に減少するだけなので、挿入すべき頂点を見逃すことは決してありません。
いつ終了するかを決定するには、 に追加した頂点の合計増加を追跡するだけでよいことに注意してください。さらに、 の場合、少なくとも 1 つの頂点のゲインはゼロではないため、常に進歩します。
成果
私たちは、サポートされている 3 つの距離メトリック (ユークリッド、コサイン、内積) をカバーする 4 つのデータセットで実験を実行しました。
- quora-E5-small: 522931文書、384次元、コサイン類似度を使用、
- cohere-wikipedia-v2: 100万文書、768次元、コサイン類似度を使用。
- 要点: 100万文書、960次元、ユークリッド距離を使用、
- cohere-wikipedia-v3: 100 万件のドキュメント、1024 次元、最大内積を使用します。
各データセットに対して、2 つの量子化レベルを評価します。
- int8 – 次元ごとに1バイトの整数を使用し、
- BBQ – 次元ごとに 1 ビットを使用します。
最後に、各実験について、2 つの検索深度で検索品質を評価し、インデックスを構築した後と、単一のセグメントに強制的にマージした後を調べます。
要約すると、グラフの品質を維持しながら、インデックス作成とマージの速度を一貫して大幅に向上させ、すべてのケースで検索パフォーマンスを実現できます。
実験1: int8量子化
ベースラインから候補、つまり提案された変更までの平均的な高速化は次のとおりです。
インデックス時間の高速化: 1.28
強制マージの高速化: 1.72
これは実行時間の次の内訳に対応する。
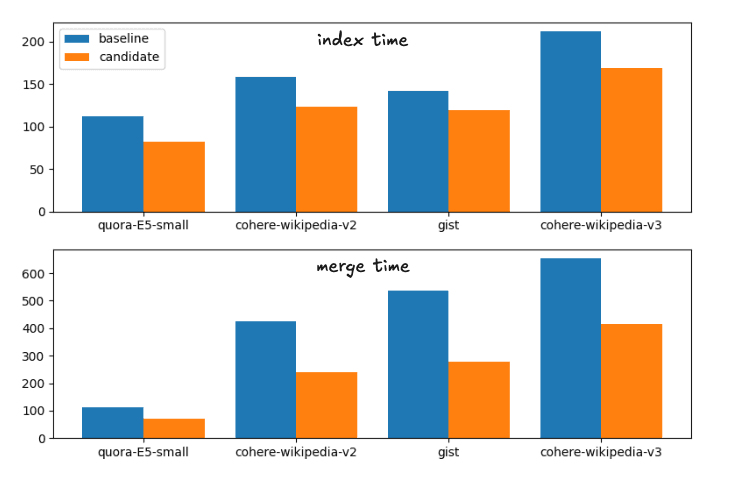
ベースラインと候補のマージ戦略のインデックスとマージ時間
完全性のために正確な時間は
| 索引 | マージ | |||
|---|---|---|---|---|
| データセット | ベースライン | 候補者 | 構築 | 候補者 |
| quora-E5-small | 112.41秒 | 81.55秒 | 113.81秒 | 70.87秒 |
| ウィキコヒアv2 | 158.1秒 | 122.95秒 | 425.20秒 | 239.28秒 |
| 要旨 | 141.82秒 | 119.26秒 | 536.07秒 | 279.05秒 |
| ウィキコヒアv3 | 211.86秒 | 168.22秒 | 654.97秒 | 414.12秒 |
以下に、複数のセグメントを持つインデックス(すべてのベクトルをインデックスした後のデフォルトのマージ戦略の最終結果)と単一セグメントへの強制マージ後のインデックスの、2 つの検索深度(recall@10 と recall@100)と、単一セグメントへの強制マージ後の、候補(破線)とベースラインを比較したリコール対レイテンシのグラフを示します。曲線が高く、左に寄っているほど良好であり、これは、より低いレイテンシでより高い再現性を意味します。
ご覧のとおり、複数のセグメント インデックスの場合、候補は Cohere v3 データセットの方が優れており、他のすべてのデータセットではわずかに劣りますが、ほぼ同等です。単一セグメントに統合した後、リコール曲線はすべてのケースでほぼ同じになります。
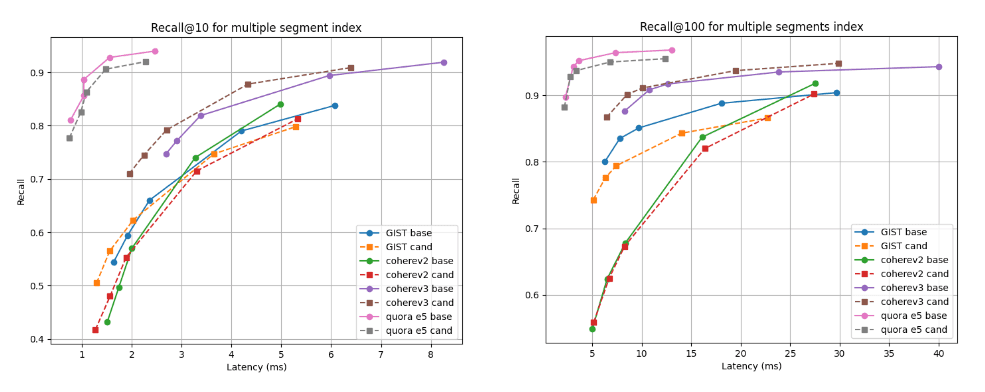
インデックス構築後のレイテンシと@10および@100の関係を思い出してください
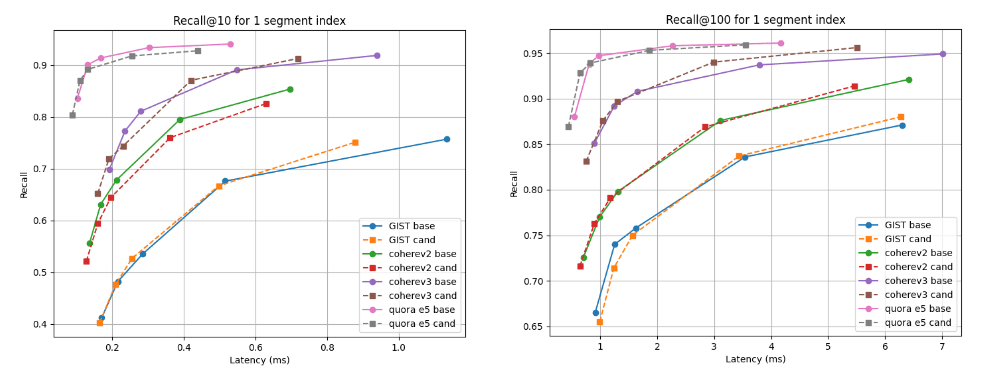
単一セグメントにマージした後のレイテンシと@10および@100のリコール
実験2:BBQ量子化
ベースラインから候補までの平均的な高速化は次のとおりです。
インデックス時間の高速化: 1.33
強制マージの高速化: 1.34
これは実行時間の次の内訳に対応する。
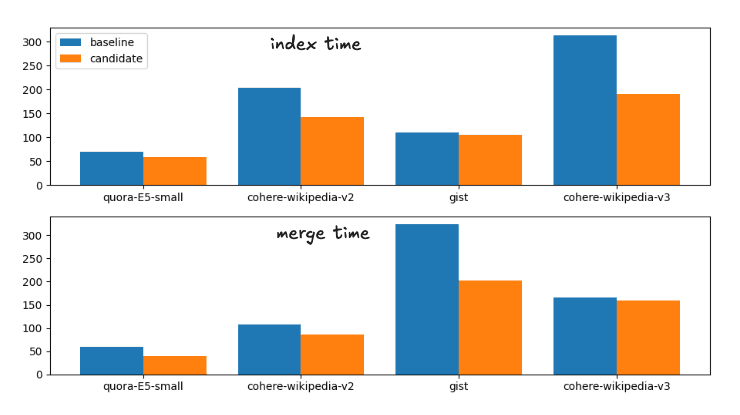
ベースラインと候補のマージ戦略のインデックスとマージ時間
完全性のために正確な時間は
| 索引 | マージ | |||
|---|---|---|---|---|
| データセット | ベースライン | 候補者 | 構築 | 候補者 |
| quora-E5-small | 70.71秒 | 58.25秒 | 59.38秒 | 40.15秒 |
| ウィキコヒアv2 | 203.08秒 | 142.27秒 | 107.27秒 | 85.68秒 |
| 要旨 | 110.35秒 | 105.52秒 | 323.66秒 | 202.2秒 |
| ウィキコヒアv3 | 313.43秒 | 190.63秒 | 165.98秒 | 159.95秒 |
複数のセグメント インデックスの場合、ベースラインがわずかに優れている cohere v2 を除き、ほぼすべてのデータセットで候補の方が優れています。単一セグメントインデックスの場合、リコール曲線はすべてのケースでほぼ同じです。
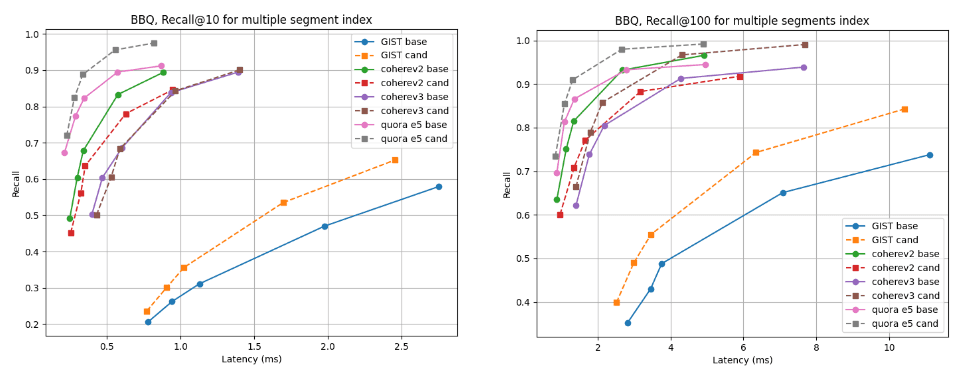
インデックス構築後のレイテンシと@10および@100の関係を思い出してください
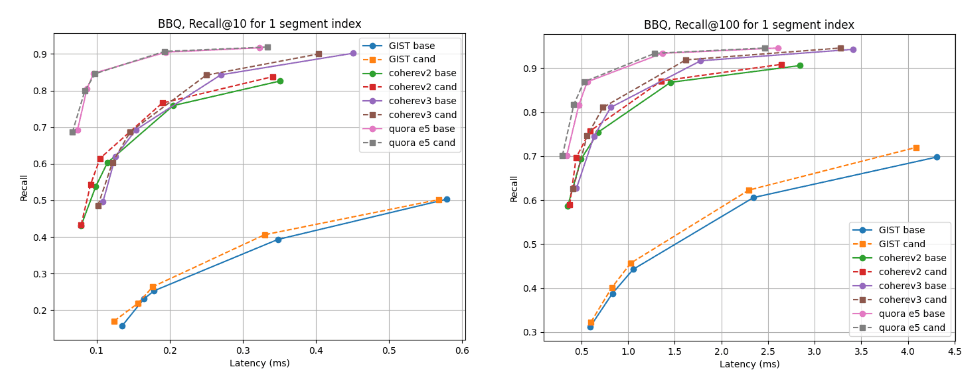
@10と@100を1つのセグメントに統合した場合のレイテンシを思い出してください
まとめ
このブログで説明したアルゴリズムは、今後リリースされる Lucene 10.2 およびそれに基づく Elasticsearch リリースで利用できるようになります。ユーザーは、これらの新しいバージョンで改善されたマージ パフォーマンスと短縮されたインデックス構築時間を活用できるようになります。この変更は、Lucene と Elasticsearch をベクター検索とハイブリッド検索に高速かつ効率的にするための継続的な取り組みの一環です。




