Elasticsearch ofrece a los desarrolladores el conjunto de herramientas de búsqueda más completo, desde la búsqueda vectorial hasta las potentes API REST. Descubre los cuadernos de muestra en GitHub para probar algo nuevo. También puedes iniciar tu prueba gratuita o ejecutar Elasticsearch localmente hoy mismo.
En el pasado, hablamos de algunos de los retos de tener que buscar en varios gráficos HNSW y cómo pudimos mitigarlos. En ese momento insinuamos algunas mejoras adicionales que planeamos. Esta publicación es la culminación de ese trabajo.
Podrías preguntarte, ¿por qué usar varios gráficos? Este es un efecto secundario de una elección arquitectónica en Lucene: segmentos inmutables. Como ocurre con la mayoría de las opciones arquitectónicas, hay pros y contras. Por ejemplo, recientemente lanzamos Elasticsearch sin servidor con GA. En este contexto, obtuvimos beneficios muy significativos de los segmentos inmutables, incluida la replicación eficiente de índices y la capacidad de desacoplar el índice y el proceso de consulta y escalarlos automáticamente de forma independiente. Para la cuantificación vectorial, las fusiones de segmentos nos dan la oportunidad de actualizar los parámetros para adaptarlos a las características de los datos. En este sentido, creemos que hay otros beneficios que ofrece tener oportunidades para medir las características de los datos y revisar las opciones de indexación.
En esta publicación, discutiremos el trabajo que estuvimos haciendo para reducir significativamente la sobrecarga de crear múltiples gráficos HNSW y, en individuo, para reducir el costo de fusionar gráficos.
Fondo
Para mantener un número manejable de segmentos, Lucene verifica periódicamente si debe fusionar segmentos. Esto equivale a comprobar si el recuento de segmentos actual supera un recuento de segmentos de destino, que está determinado por el tamaño del segmento base y la política de combinación. Si se supera el recuento, Lucene combina grupos de segmentos mientras se infringe la restricción. Este proceso se describió en detalle en otra parte.
Lucene elige fusionar segmentos de tamaño similar porque esto logra un crecimiento logarítmico en la amplificación de escritura. En el caso de un índice vectorial, la amplificación de escritura es el número de veces que se insertará un vector en un gráfico. Lucene intentará fusionar segmentos en grupos de aproximadamente 10. En consecuencia, los vectores se insertan en un gráfico aproximadamente veces, donde es el recuento de vectores índice y es el recuento de vectores de segmento base esperado. Debido al crecimiento logarítmico, la amplificación de escritura es de un solo dígito incluso para índices enormes. Sin embargo, el tiempo total dedicado a fusionar gráficos es linealmente proporcional a la amplificación de escritura.
Al fusionar gráficos HNSW ya hacemos una pequeña optimización: retener el gráfico para el segmento más grande e insertar vectores de los otros segmentos en él. Esta es la razón del factor 9/10 anterior. A continuación, mostramos cómo podemos hacerlo significativamente mejor empleando información de todos los gráficos que estamos fusionando.
Fusión de grafos HNSW
Antes conservábamos el grafo más grande e insertábamos vectores de los otros ignorando los gráficos que los contenían. La idea clave que aprovechamos a continuación es que cada grafo HNSW que descartamos contiene información importante de proximidad sobre los vectores que contiene. Nos gustaría usar esta información para acelerar la inserción, al menos algunos, de los vectores.
Nos enfocamos en el problema de insertar un gráfico más pequeño en un gráfico más grande , ya que esta es una operación atómica que podemos usar para construir cualquier política de combinación.
La estrategia consiste en encontrar un subconjunto de vértices de insertarlos en el gráfico grande. Luego usamos la conectividad de estos vértices en el gráfico pequeño para acelerar la inserción de los vértices restantes . A continuación, usamos y para denotar los vecinos de un vértice en el grafo pequeño y grande, respectivamente. Esquemáticamente, el proceso es el siguiente.
MERGE-HNSW
Inputs and
1Find to insert into using COMPUTE-JOIN-SET2Insert each vertex into 3for do456FAST-SEARCH-LAYER7SELECT-NEIGHBORS-HEURISTIC8
Calculamos el conjunto empleando un procedimiento que discutimos a continuación (línea 1). Luego insertamos cada vértice en en el gráfico grande usando el procedimiento de inserción HNSW estándar (línea 2). Para cada vértice que no insertamos encontramos sus vecinos que insertamos y sus vecinos en el gráfico grande (líneas 4 y 5). Usamos un procedimiento FAST-SEARCH-LAYER sembrado con este conjunto (línea 6) para encontrar los candidatos para el SELECT-NEIGHBORS-HEURISTIC del artículo HNSW (línea 7). En efecto, estamos reemplazando SEARCH-LAYER para encontrar el conjunto candidato en el método INSERT (Algoritmo 1 del artículo), que de lo contrario no cambia. Finalmente, agregamos el vértice que acabamos de insertar en (línea 8).
Está claro que para que esto funcione, cada vértice en debe tener al menos un vecino en . De hecho, requerimos que para cada vértice en que para algunos , la máxima conectividad de capa. Observamos que en los gráficos reales de HNSW vemos una gran dispersión de grados de vértice. La siguiente figura muestra una función de densidad acumulativa típica del grado de vértice para la capa inferior de un gráfico HNSW de Lucene.
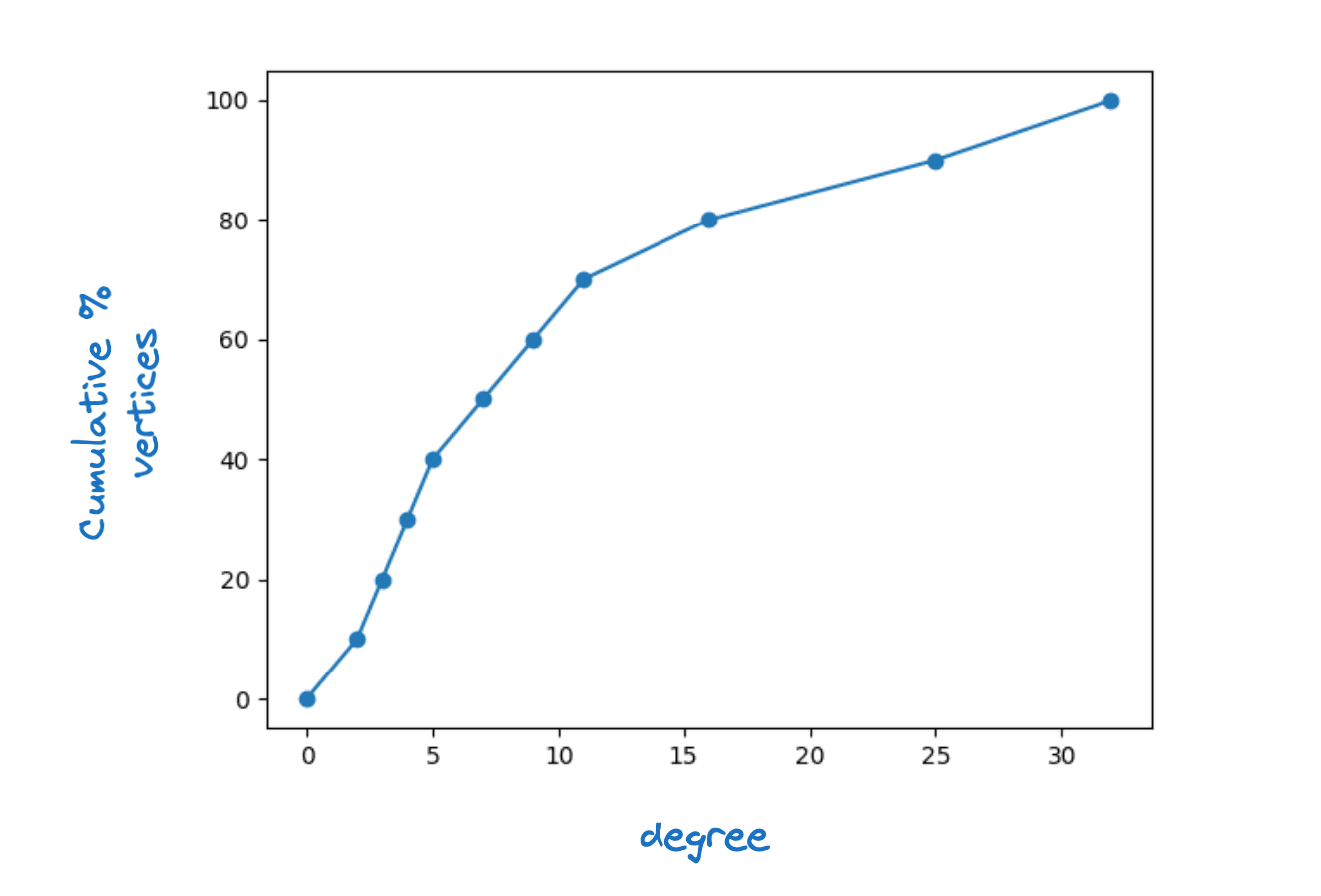
Ejemplo de distribución de grados de vértice
Exploramos el uso de un valor fijo para así como convertirlo en una función del grado del vértice. Esta segunda opción conduce a mayores aceleramientos con un impacto mínimo en la calidad del gráfico, por lo que optó por lo siguiente
Tenga en cuenta que | es igual al grado del vértice en el gráfico pequeño por definición. Tener un límite inferior de dos significa que insertaremos cada vértice cuyo grado sea menor que dos.
Un argumento de conteo simple sugiere que si elegimos con cuidado, solo necesitamos insertar alrededor en directamente. Específicamente, coloreamos una arista del grafo si insertamos exactamente uno de sus vértices finales en . Entonces sabemos que para que cada vértice en tenga al menos vecinos en , necesitamos colorear al menos aristas. Además, esperamos que
Aquí, es el grado medio del vértice en la gráfica pequeña. Para cada vértice coloreamos como máximo Bordes. Por lo tanto, el número total de bordes que esperamos colorear es como máximo |J|\, \mathbb{E}_U\left[|N_s(U)|\derecha]. Esperamos que al elegir con cuidado coloreemos cerca de este número de aristas y así cubrir todos los vértices necesidades para satisfacer
Esto implica que .
Siempre que SEARCH-LAYER domine el tiempo de ejecución, esto sugiere que podríamos lograr un aceleramiento de hasta en el tiempo de fusión. Dado el crecimiento logarítmico de la amplificación de escritura, esto significa que incluso para índices muy grandes, normalmente solo duplicaríamos el tiempo de construcción en comparación con la construcción de un gráfico.
El riesgo en esta estrategia es que dañamos la calidad del gráfico. Inicialmente lo intentamos con un FAST-SEARCH-LAYERsin operación. Descubrimos que esto degrada la calidad del gráfico en la medida en que la recuperación en función de la latencia se vio afectada, particularmente cuando se fusiona en un solo segmento. Luego exploramos varias alternativas empleando una búsqueda limitada del gráfico. Al final, la elección más efectiva fue la más simple. Usar SEARCH-LAYER pero con un ef_constructionbajo. Con esta parametrización pudimos lograr gráficos de excelente calidad y aún así disminuir el tiempo de fusión en un poco más del 30% en promedio.
Cálculo del conjunto de unión
Encontrar un buen conjunto de unión puede formular como un problema de cobertura de grafos HNSW. Una heurística codiciosa es una heurística simple y efectiva para aproximar cubiertas óptimas de grafos. El enfoque que tomamos elige vértices uno a uno para sumar a en orden decreciente de ganancia. La ganancia se define de la siguiente manera:
Aquí, denota el recuento de vecinos de un vector en y es la función indicadora. La ganancia incluye el cambio en el recuento del vértice que agregamos a , es decir, ya que nos acercamos a nuestro objetivo al agregar un vértice menos cubierto. El cálculo de la ganancia se ilustra en la siguiente figura para el vértice naranja central.
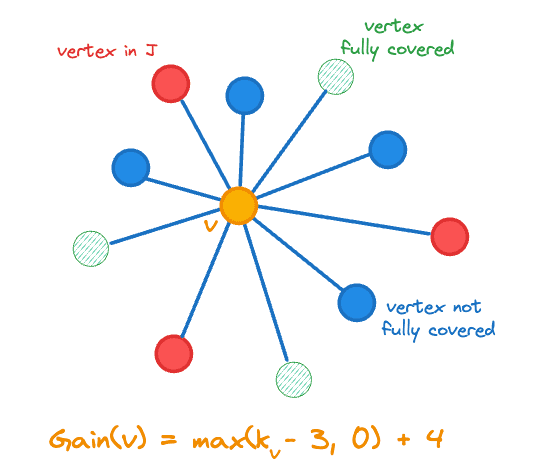
Ganancia de vértice para agregar al conjunto de unión J
Mantenemos el siguiente estado para cada vértice :
- Ya sea rancio,
- Su ganancia
- El recuento de vértices adyacentes en denotado
- Un número aleatorio en el rango [0,1] que se usa para el desempate.
El pseudocódigo para calcular el conjunto de combinaciones es el siguiente.
COMPUTE-JOIN-SET
Inputs
123for do4567while do
8 maximum gain vertex in 9Remove the state for from 10if is not stale then111213for do14mark as stale if 15mark neighbors of stale if
16
17else
18
19if then
20
21return
Primero inicializamos el estado en las líneas 1-5.
En cada iteración del bucle principal extraemos inicialmente el vértice de ganancia máxima (línea 8), rompiendo los empates al azar. Antes de realizar cualquier cambio, debemos verificar si la ganancia del vértice está obsoleta. En individuo, cada vez que agregamos un vértice a afectamos la ganancia de otros vértices:
- Dado que todos sus vecinos tienen un vecino adicional en , sus ganancias pueden cambiar (línea 14)
- Si alguno de sus vecinos ahora está completamente cubierto, todas las ganancias de sus vecinos pueden cambiar (líneas 14-16)
Recalculamos las ganancias de manera perezosa, por lo que solo recalculamos la ganancia de un vértice si queremos insertarlo en (líneas 18-20). Dado que las ganancias solo disminuyen, nunca podemos perder un vértice que debamos insertar.
Tenga en cuenta que simplemente necesitamos realizar un seguimiento de la ganancia total de vértices que agregamos a para determinar cuándo salir. Además, al menos un vértice tendrá una ganancia distinta de cero, por lo que siempre progresamos.
Resultados
Realizamos experimentos en cuatro conjuntos de datos que juntos cubren nuestras tres métricas de distancia admitidas (euclidiana, coseno y producto interno):
- quora-E5-small: 522931 documentos, 384 dimensiones y emplea la similitud del coseno,
- cohe-wikipedia-v2: 1M de documentos, 768 dimensiones y emplea similitud de coseno,
- gist: 1M documentos, 960 dimensiones y emplea la distancia euclidiana, y
- cohe-wikipedia-v3: 1M de documentos, 1024 dimensiones y emplea el máximo producto interno.
Para cada conjunto de datos evaluamos dos niveles de cuantificación:
- int8: que emplea un entero de 1 byte por dimensión y
- BBQ: que emplea un solo bit por dimensión.
Finalmente, para cada experimento evaluamos la calidad de la búsqueda a dos profundidades de recuperación y examinamos luego de construir el índice y luego luego de forzar la fusión en un solo segmento.
En resumen, logramos aceleramientos sustanciales consistentes en la indexación y la fusión mientras mantenemos la calidad del gráfico y, por lo tanto, el rendimiento de búsqueda en todos los casos.
Experimento 1: cuantización int8
Los aceleramientos promedio desde la línea de base hasta el candidato, los cambios propuestos, son:
Aceleramiento del tiempo del índice: 1.28
Forzar la velocidad de combinación: 1.72
Esto corresponde al siguiente desglose en tiempos de ejecución
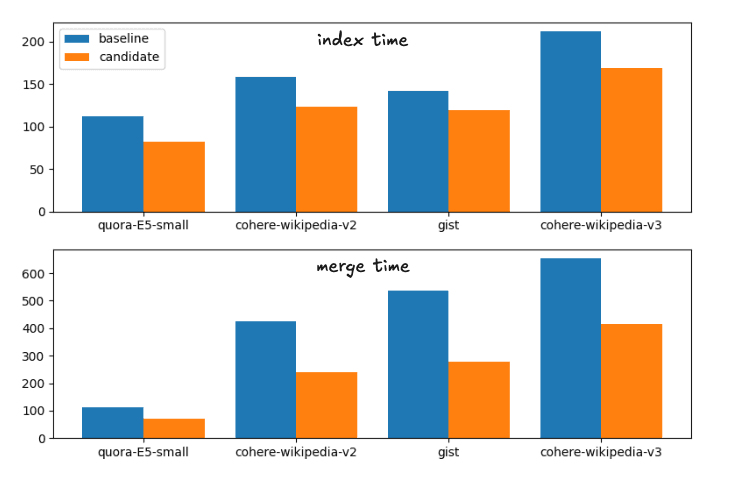
Indexar y fusionar tiempos para las estrategias de fusión de línea base y candidatas
Para completar, los tiempos exactos son
| Índice | Fusionar | |||
|---|---|---|---|---|
| Conjunto de datos | referencia | candidato | Desarrolla | candidato |
| quora-E5-pequeño | 112.41s | 81.55s | 113.81s | 70.87s |
| wiki-cohesión-v2 | 158.1s | 122,95 segundos | 425.20s | 239.28s |
| quid | 141.82s | 119.26s | 536.07s | 279.05s |
| wiki-cohesión-v3 | 211.86s | 168.22s | 654,97 segundos | 414.12s |
A continuación, mostramos los gráficos de recuperación frente a latencia que comparan el candidato (líneas discontinuas) con la línea de base en dos profundidades de recuperación: recall@10 y recall@100 para índices con múltiples segmentos (el resultado final de nuestra estrategia de fusión predeterminada luego de indexar todos los vectores) y luego de forzar la fusión en un solo segmento. Una curva más alta y más a la izquierda es mejor, lo que significa una mayor recuperación con una latencia más baja.
Como puede ver, para índices de múltiples segmentos, el candidato es mejor para el conjunto de datos Cohere v3 y un poco peor, pero casi comparable, para todos los demás conjuntos de datos. Luego de fusionar en un solo segmento, las curvas de recuperación son casi idénticas para todos los casos.
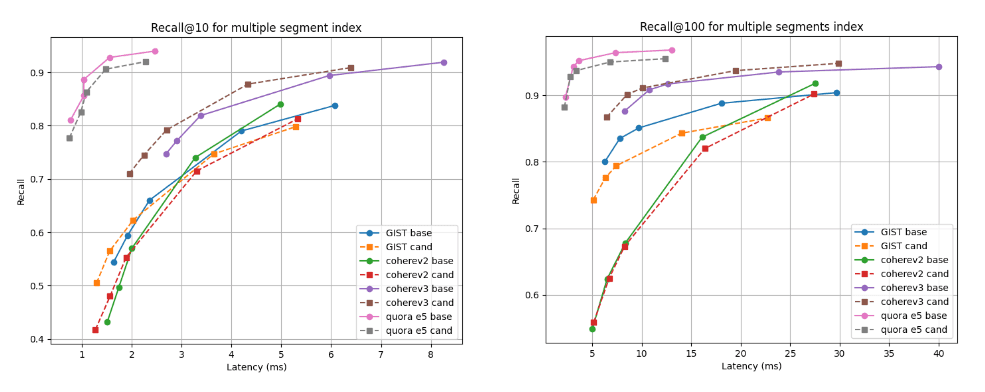
Recuperar @10 y @100 frente a la latencia luego de crear el índice
Recuperar @10 y @100 frente a la latencia luego de fusionar en un solo segmento
Experimento 2: Cuantización de asado
Los aceleramientos promedio desde la línea de base hasta el candidato son:
Aceleramiento del tiempo de índice: 1.33
Forzar la velocidad de combinación: 1.34
Esto corresponde al siguiente desglose en tiempos de ejecución
Indexar y fusionar el tiempo para las estrategias de fusión de línea base y candidatas
Para completar, los tiempos exactos son
| Índice | Fusionar | |||
|---|---|---|---|---|
| Conjunto de datos | referencia | candidato | Desarrolla | candidato |
| quora-E5-pequeño | 70.71s | 58.25s | 59.38s | 40.15s |
| wiki-cohesión-v2 | 203.08s | 142.27s | 107.27s | 85.68s |
| quid | 110.35s | 105,52 segundos | 323,66 segundos | 202.2s |
| wiki-cohesión-v3 | 313.43s | 190.63s | 165,98 segundos | 159,95 segundos |
Para índices de segmentos múltiples, el candidato es mejor para casi todos los conjuntos de datos, excepto cohere v2, donde la línea de base es ligeramente mejor. Para los índices de un solo segmento, las curvas de recuperación son casi idénticas para todos los casos.
Recuperar @10 y @100 frente a la latencia luego de crear el índice
Recordar @10 y @100 frente a la latencia que se fusionó en un solo segmento
Conclusión
El algoritmo discutido en este blog estará disponible en el próximo Lucene 10.2 y en la versión de Elasticsearch que se basa en él. Los usuarios podrán aprovechar el rendimiento mejorado de la combinación y el tiempo de compilación de índices reducido en estas nuevas versiones. Este cambio es parte de nuestro esfuerzo continuo para hacer que Lucene y Elasticsearch sean rápidos y eficientes para la búsqueda vectorial e híbrida.




