Da busca vetorial às poderosas REST APIs, o Elasticsearch oferece aos desenvolvedores o kit de ferramentas de busca mais abrangente. Mergulhe em notebooks de exemplo no GitHub para experimentar algo novo. Você também pode iniciar seu teste gratuito ou executar o Elasticsearch localmente hoje mesmo.
No passado, discutimos alguns dos desafios de ter que pesquisar em vários grafos HNSW e como conseguimos mitigá-los. Naquela ocasião, mencionamos algumas melhorias adicionais que tínhamos planejado. Este post é o culminar desse trabalho.
Você pode perguntar: por que usar vários gráficos? Este é um efeito colateral de uma escolha arquitetônica no Lucene: segmentos imutáveis. Como acontece com a maioria das escolhas arquitetônicas, há prós e contras. Por exemplo, recentemente disponibilizamos o Elasticsearch sem servidor. Nesse contexto, obtivemos benefícios muito significativos de segmentos imutáveis, incluindo replicação de índice eficiente e a capacidade de desacoplar índice e computação de consulta e dimensioná-los automaticamente de forma independente. Para quantização vetorial, as fusões de segmentos nos dão a oportunidade de atualizar parâmetros para adaptá-los às características dos dados. Nessa linha, acreditamos que há outras vantagens proporcionadas pela oportunidade de medir características de dados e revisitar opções de indexação.
Nesta postagem, discutiremos o trabalho que temos feito para reduzir significativamente a sobrecarga de construção de vários gráficos HNSW e, em particular, para reduzir o custo de mesclagem de gráficos.
Histórico
Para manter um número gerenciável de segmentos, o Lucene verifica periodicamente se deve mesclar segmentos. Isso equivale a verificar se a contagem de segmentos atual excede uma contagem de segmentos de destino, que é determinada pelo tamanho do segmento base e pela política de mesclagem. Se a contagem for excedida, o Lucene mescla grupos de segmentos enquanto a restrição for violada. Este processo foi descrito em detalhes em outro lugar.
Lucene opta por mesclar segmentos de tamanhos semelhantes porque isso atinge um crescimento logarítmico na amplificação de gravação. No caso de um índice vetorial, a amplificação de escrita é o número de vezes que um vetor será inserido em um gráfico. O Lucene tentará mesclar segmentos em grupos de aproximadamente 10. Consequentemente, os vetores são inseridos em um gráfico aproximadamente vezes, onde é a contagem do vetor de índice e é a contagem do vetor de segmento base esperado. Devido ao crescimento logarítmico, a amplificação da gravação é de um dígito, mesmo para índices grandes. Entretanto, o tempo total gasto na fusão de gráficos é linearmente proporcional à amplificação da gravação.
Ao mesclar gráficos HNSW, já fazemos uma pequena otimização: mantendo o gráfico do maior segmento e inserindo vetores dos outros segmentos nele. Esta é a razão do fator 9/10 acima. Abaixo mostramos como podemos melhorar significativamente usando informações de todos os gráficos que estamos mesclando.
Fusão de gráficos HNSW
Anteriormente, mantínhamos o grafo maior e inseríamos vetores dos demais, ignorando os grafos que os continham. A principal conclusão que utilizamos a seguir é que cada grafo HNSW descartado contém informações importantes sobre a proximidade dos vetores que ele contém. Gostaríamos de usar essas informações para acelerar a inserção, pelo menos de alguns, dos vetores.
Nós nos concentramos no problema de inserir um gráfico menor em um gráfico maior , já que esta é uma operação atômica que podemos usar para construir qualquer política de mesclagem.
A estratégia é encontrar um subconjunto de vértices de para inserir no gráfico grande. Em seguida, usamos a conectividade desses vértices no pequeno gráfico para acelerar a inserção dos vértices restantes . A seguir, usamos e para denotar os vizinhos de um vértice no gráfico pequeno e grande, respectivamente. Esquematicamente o processo é o seguinte.
MERGE-HNSW
Inputs and
1Find to insert into using COMPUTE-JOIN-SET2Insert each vertex into 3for do456FAST-SEARCH-LAYER7SELECT-NEIGHBORS-HEURISTIC8
Calculamos o conjunto usando um procedimento que discutiremos abaixo (linha 1). Em seguida, inserimos cada vértice em no gráfico grande usando o procedimento de inserção padrão HNSW (linha 2). Para cada vértice que não inserimos, encontramos seus vizinhos que inserimos e seus vizinhos no gráfico grande (linhas 4 e 5). Usamos um procedimento FAST-SEARCH-LAYER semeado com este conjunto (linha 6) para encontrar os candidatos para o SELECT-NEIGHBORS-HEURISTIC do artigo HNSW (linha 7). Na verdade, estamos substituindo SEARCH-LAYER para encontrar o conjunto de candidatos no método INSERT (Algoritmo 1 do artigo), que de outra forma não será alterado. Por fim, adicionamos o vértice que acabamos de inserir em (linha 8).
É claro que para que isso funcione, cada vértice em deve ter pelo menos um vizinho em . Na verdade, exigimos que para cada vértice em que para algum , a conectividade máxima da camada. Observamos que em gráficos HNSW reais vemos uma grande dispersão de graus de vértices. A figura abaixo mostra uma função de densidade cumulativa típica do grau do vértice para a camada inferior de um gráfico Lucene HNSW.
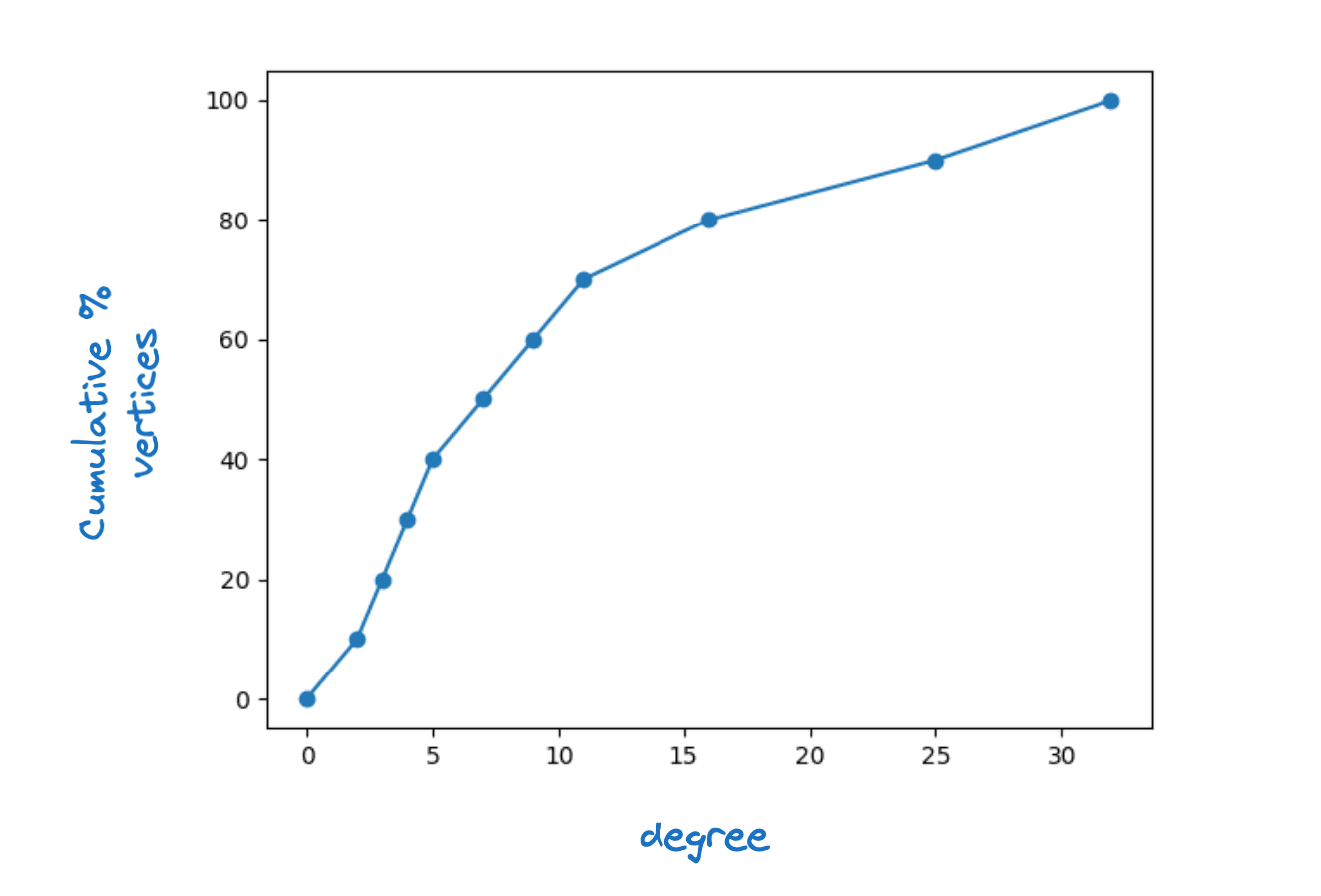
Exemplo de distribuição de graus de vértices
Exploramos o uso de um valor fixo para e também o tornamos uma função do grau do vértice. Esta segunda opção leva a maiores acelerações com impacto mínimo na qualidade do gráfico, então optei pela seguinte opção
Observe que | é igual ao grau do vértice no gráfico pequeno por definição. Ter um limite inferior de dois significa que inseriremos todos os vértices cujo grau seja menor que dois.
Um argumento de contagem simples sugere que se escolhermos cuidadosamente, precisamos apenas inserir em torno de em diretamente. Especificamente, colorimos uma aresta do gráfico se inserirmos exatamente um de seus vértices finais em . Então sabemos que para cada vértice em ter pelo menos vizinhos em precisamos colorir pelo menos arestas. Além disso, esperamos que
Aqui, é o grau médio do vértice no pequeno gráfico. Para cada vértice colorimos no máximo arestas. Portanto, o número total de arestas que esperamos colorir é no máximo . Esperamos que, ao escolher cuidadosamente, possamos colorir perto desse número de arestas e, portanto, para cobrir todos os vértices, precisa satisfazer
Isso implica que .
Se SEARCH-LAYER dominar o tempo de execução, isso sugere que poderíamos atingir uma velocidade de até maior no tempo de mesclagem. Dado o crescimento logarítmico da amplificação de gravação, isso significa que mesmo para índices muito grandes, normalmente dobraríamos apenas o tempo de construção em comparação à construção de um gráfico.
O risco dessa estratégia é que prejudicamos a qualidade do gráfico. Inicialmente tentamos com um no-op FAST-SEARCH-LAYER. Descobrimos que isso degrada a qualidade do gráfico a ponto de a recuperação como função da latência ser impactada, principalmente ao mesclar em um único segmento. Em seguida, exploramos várias alternativas usando uma busca limitada do gráfico. No final, a escolha mais eficaz foi a mais simples. Use SEARCH-LAYER mas com um ef_construction baixo. Com essa parametrização conseguimos obter gráficos de excelente qualidade e ainda diminuir o tempo de mesclagem em pouco mais de 30% em média.
Calculando o conjunto de junção
Encontrar um bom conjunto de junção pode ser formulado como um problema de cobertura de grafos HNSW. Uma heurística gulosa é uma heurística simples e eficaz para aproximar coberturas ótimas de grafos. A abordagem que adotamos seleciona os vértices um de cada vez para adicionar a em ordem decrescente de ganho. O ganho é definido da seguinte forma:
Aqui, denota a contagem de vizinhos de um vetor em e é a função indicadora. O ganho inclui a mudança na contagem do vértice que adicionamos a , ou seja, , pois nos aproximamos do nosso objetivo adicionando um vértice menos coberto. O cálculo do ganho é ilustrado na figura abaixo para o vértice central laranja.
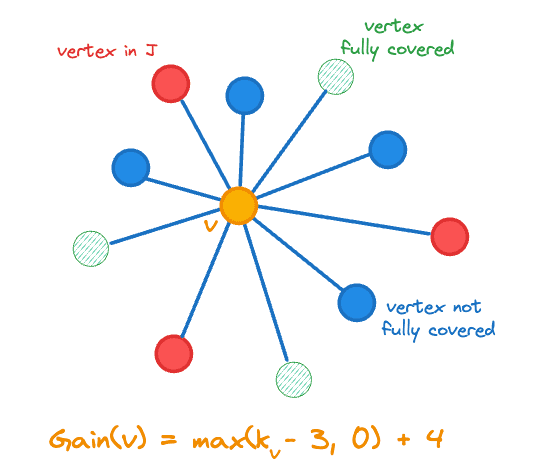
Ganho de vértice para adicionar ao conjunto de junção J
Mantemos o seguinte estado para cada vértice :
- Seja velho,
- Seu ganho ,
- A contagem de vértices adjacentes em denotada por ,
- Um número aleatório no intervalo [0,1] que é usado para desempate.
O pseudocódigo para calcular o conjunto de junções é o seguinte.
COMPUTE-JOIN-SET
Inputs
123for do4567while do
8 maximum gain vertex in 9Remove the state for from 10if is not stale then111213for do14mark as stale if 15mark neighbors of stale if
16
17else
18
19if then
20
21return
Primeiro inicializamos o estado nas linhas 1-5.
Em cada iteração do loop principal, extraímos inicialmente o vértice de ganho máximo (linha 8), desfazendo empates aleatoriamente. Antes de fazer qualquer alteração, precisamos verificar se o ganho do vértice está obsoleto. Em particular, cada vez que adicionamos um vértice em , afetamos o ganho de outros vértices:
- Como todos os seus vizinhos têm um vizinho adicional em seus ganhos podem mudar (linha 14)
- Se algum dos seus vizinhos estiver agora totalmente coberto, os ganhos de todos os seus vizinhos podem mudar (linhas 14-16)
Nós recalculamos os ganhos de forma lenta, então só recalculamos o ganho de um vértice se quisermos inseri-lo em (linhas 18-20). Como os ganhos sempre diminuem, nunca podemos perder um vértice que devemos inserir.
Observe que precisamos apenas monitorar o ganho total de vértices que adicionamos a para determinar quando sair. Além disso, enquanto pelo menos um vértice terá ganho diferente de zero, então sempre progredimos.
Resultados
Realizamos experimentos em quatro conjuntos de dados que juntos abrangem nossas três métricas de distância suportadas (euclidiana, cosseno e produto interno):
- quora-E5-small: 522931 documentos, 384 dimensões e usa similaridade de cosseno,
- cohere-wikipedia-v2: 1 milhão de documentos, 768 dimensões e usa similaridade de cosseno,
- gist: 1M documentos, 960 dimensões e utiliza distância euclidiana e
- cohere-wikipedia-v3: 1 milhão de documentos, 1.024 dimensões e usa o produto interno máximo.
Para cada conjunto de dados, avaliamos dois níveis de quantização:
- int8 – que usa um inteiro de 1 byte por dimensão e
- Churrasco – que usa um único bit por dimensão.
Por fim, para cada experimento, avaliamos a qualidade da pesquisa em duas profundidades de recuperação e examinamos depois da construção do índice e depois da fusão forçada em um único segmento.
Em resumo, alcançamos acelerações substanciais e consistentes na indexação e mesclagem, mantendo a qualidade do gráfico e, consequentemente, o desempenho da pesquisa em todos os casos.
Experimento 1: quantização int8
As acelerações médias da linha de base até o candidato, as mudanças propostas, são:
Aceleração do tempo de índice: 1,28
Forçar aceleração de fusão: 1,72
Isso corresponde à seguinte repartição nos tempos de execução
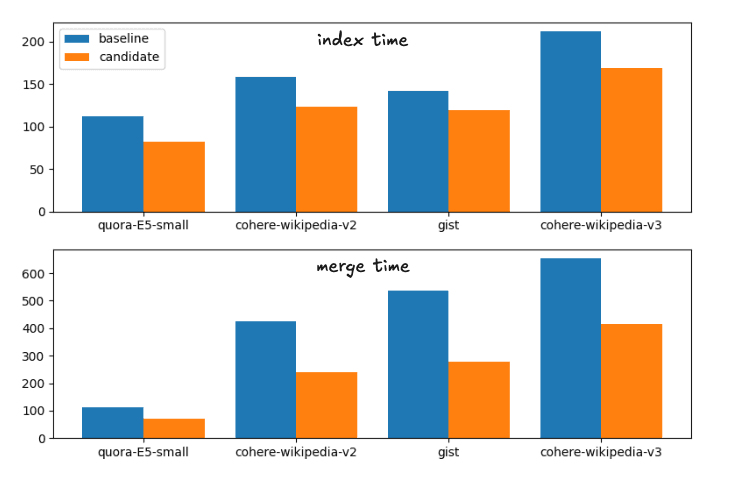
Tempos de indexação e mesclagem para as estratégias de mesclagem de base e candidatas
Para completar, os horários exatos são
| Índice | Mesclar | |||
|---|---|---|---|---|
| Conjunto de dados | linha de base | candidato | Criar | candidato |
| quora-E5-pequeno | 112,41s | 81,55s | 113,81s | 70,87s |
| wiki-cohere-v2 | 158,1s | 122,95s | 425,20s | 239,28s |
| essência | 141,82s | 119,26s | 536,07s | 279,05s |
| wiki-cohere-v3 | 211,86s | 168,22s | 654,97s | 414,12s |
Abaixo, mostramos os gráficos de recall versus latência que comparam o candidato (linhas tracejadas) à linha de base em duas profundidades de recuperação: recall@10 e recall@100 para índices com vários segmentos (o resultado final da nossa estratégia de mesclagem padrão após indexar todos os vetores) e após a mesclagem forçada para um único segmento. Uma curva mais alta e mais à esquerda é melhor, o que significa maior recuperação com menor latência.
Como você pode ver, para índices de múltiplos segmentos, o candidato é melhor para o conjunto de dados Cohere v3 e um pouco pior, mas quase comparável, para todos os outros conjuntos de dados. Após a fusão em um único segmento, as curvas de recall são quase idênticas para todos os casos.
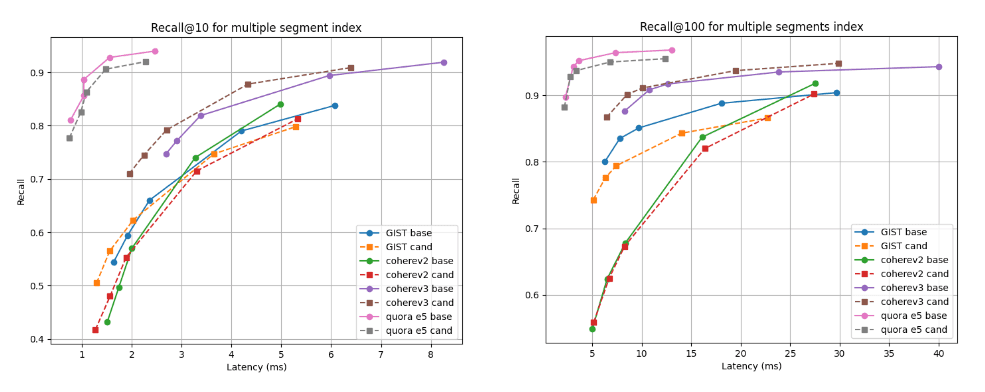
Lembre-se de @10 e @100 vs latência após a construção do índice
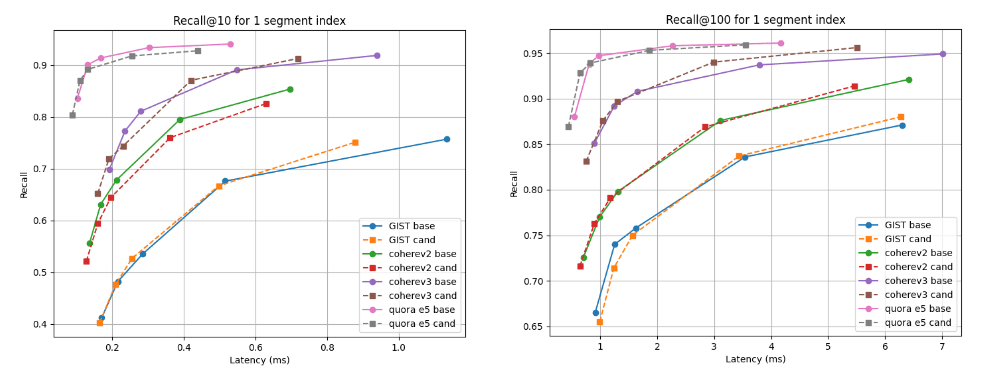
Lembre-se de @10 e @100 vs latência após a fusão em um único segmento
Experimento 2: quantização BBQ
As acelerações médias da linha de base até o candidato são:
Aceleração do tempo de índice: 1,33
Forçar aceleração de fusão: 1,34
Isso corresponde à seguinte repartição nos tempos de execução
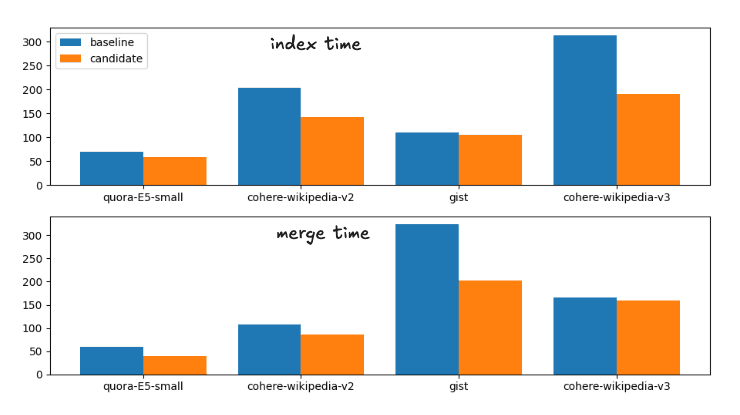
Índice e tempo de mesclagem para as estratégias de mesclagem de base e candidatas
Para completar, os horários exatos são
| Índice | Mesclar | |||
|---|---|---|---|---|
| Conjunto de dados | linha de base | candidato | Criar | candidato |
| quora-E5-pequeno | 70,71s | 58,25s | 59,38s | 40,15s |
| wiki-cohere-v2 | 203,08s | 142,27s | 107,27s | 85,68s |
| essência | 110,35s | 105,52s | 323,66s | 202,2s |
| wiki-cohere-v3 | 313,43s | 190,63s | 165,98s | 159,95s |
Para índices de múltiplos segmentos, o candidato é melhor para quase todos os conjuntos de dados, exceto o Cohere v2, onde a linha de base é ligeiramente melhor. Para os índices de segmento único, as curvas de recall são quase idênticas para todos os casos.
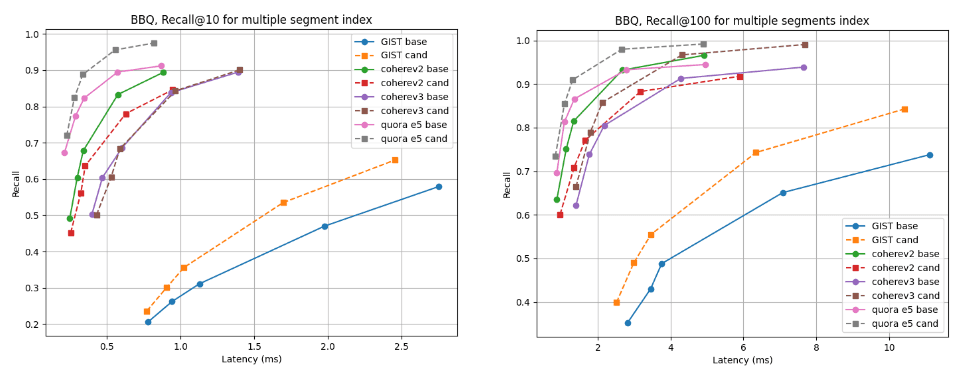
Lembre-se de @10 e @100 vs latência após a construção do índice
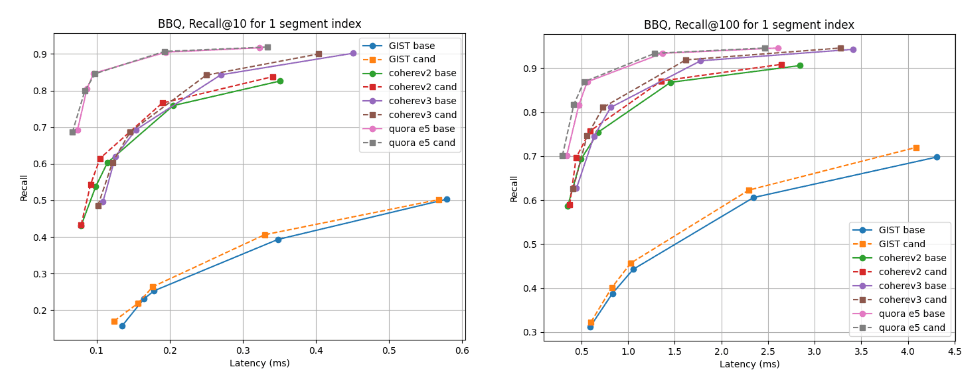
Lembre-se de @10 e @100 vs latência tendo sido mesclados em um único segmento
Conclusão
O algoritmo discutido neste blog estará disponível no próximo Lucene 10.2 e na versão do Elasticsearch baseada nele. Os usuários poderão aproveitar o desempenho de mesclagem aprimorado e o tempo reduzido de criação de índice nessas novas versões. Essa mudança faz parte do nosso esforço contínuo para tornar o Lucene e o Elasticsearch rápidos e eficientes para pesquisas vetoriais e híbridas.




