벡터 검색부터 강력한 REST API까지, Elasticsearch는 개발자에게 가장 폭넓은 검색 도구 키트를 제공합니다. GitHub의 샘플 노트북을 살펴보고 새로운 기능을 시험해 보세요. 무료 체험판을 시작하거나 지금 바로 Elasticsearch를 로컬에서 실행할 수도 있습니다.
과거에는 여러 개의 HNSW 그래프를 검색해야 할 때 발생하는 몇 가지 문제와 이를 완화할 수 있는 방법에 대해 논의한적이 있습니다. 당시 저희는 계획했던 몇 가지 추가 개선 사항을 암시했습니다. 이 게시물은 그 작업의 정점입니다.
왜 여러 개의 그래프를 사용해야 하나요? 이는 불변 세그먼트라는 루씬의 아키텍처 선택에 따른 부작용입니다. 대부분의 아키텍처 선택과 마찬가지로 장단점이 있습니다. 예를 들어, 저희는 최근에 서버리스 Elasticsearch를 정식 버전으로 출시했습니다. 이러한 맥락에서 우리는 효율적인 인덱스 복제, 인덱스와 쿼리 계산을 분리하고 독립적으로 자동 확장하는 기능 등 불변 세그먼트를 통해 매우 중요한 이점을 얻었습니다. 벡터 양자화의 경우 세그먼트 병합을 통해 데이터 특성에 맞게 파라미터를 업데이트할 수 있습니다. 이러한 맥락에서 데이터 특성을 측정하고 인덱싱 선택을 재검토할 수 있는 기회를 갖는다는 것은 다른 장점도 있다고 생각합니다.
이 글에서는 여러 개의 HNSW 그래프를 작성하는 데 드는 오버헤드를 크게 줄이고 특히 그래프를 병합하는 데 드는 비용을 줄이기 위해 수행한 작업에 대해 설명합니다.
배경
관리 가능한 세그먼트 수를 유지하기 위해 Lucene은 주기적으로 세그먼트를 병합해야 하는지 여부를 확인합니다. 이는 현재 세그먼트 수가 기본 세그먼트 크기와 병합 정책에 따라 결정되는 목표 세그먼트 수를 초과하는지 확인하는 것과 같습니다. 개수를 초과하면 제약 조건을 위반하는 동안 Lucene은 세그먼트 그룹을 병합합니다. 이 프로세스는 다른 곳에 자세히 설명되어 있습니다.
Lucene은 쓰기 증폭에서 대수적 증가를 달성하기 때문에 비슷한 크기의 세그먼트를 병합하는 방법을 선택합니다. 벡터 인덱스의 경우 쓰기 증폭은 벡터가 그래프에 삽입되는 횟수입니다. Lucene은 약 10개의 그룹으로 세그먼트를 병합하려고 시도합니다. 결과적으로 벡터는 대략 1+\frac{9}{10}\log_{10}\left (\frac{n}{n_0}\right ) 번 그래프에 삽입되며, 여기서 인덱스 벡터 수이고 예상되는 기본 세그먼트 벡터 수입니다. 대수적 증가로 인해 쓰기 증폭은 거대한 인덱스의 경우에도 한 자릿수입니다. 그러나 그래프를 병합하는 데 소요되는 총 시간은 쓰기 증폭에 선형적으로 비례합니다.
HNSW 그래프를 병합할 때 가장 큰 세그먼트의 그래프를 유지하고 다른 세그먼트의 벡터를 삽입하는 작은 최적화를 이미 수행했습니다. 이것이 위의 9/10 요소의 이유입니다. 아래에서는 병합하는 모든 그래프의 정보를 사용하여 훨씬 더 나은 결과를 얻을 수 있는 방법을 보여줍니다.
HNSW 그래프 병합
이전에는 가장 큰 그래프를 유지하고 벡터가 포함된 그래프를 무시하고 다른 그래프에서 벡터를 삽입했습니다. 아래에서 사용하는 핵심 인사이트는 우리가 폐기하는 각 HNSW 그래프에 포함된 벡터에 대한 중요한 근접성 정보가 포함되어 있다는 것입니다. 이 정보를 사용하여 적어도 일부 벡터의 삽입을 가속화하고자 합니다.
병합 정책을 구축하는 데 사용할 수 있는 원자 연산이므로 작은 그래프 )를 큰 그래프 )에 삽입하는 문제에 중점을 둡니다.
전략은 큰 그래프에 삽입할 정점 하위 집합을 찾는 것입니다. 그런 다음 작은 그래프에서 이러한 정점의 연결성을 사용하여 나머지 정점 삽입하는 속도를 높입니다. 아래에서는 작은 그래프와 큰 그래프에서 각각 및 를 사용하여 정점 이웃을 나타냅니다. 프로세스를 개략적으로 설명하면 다음과 같습니다.
MERGE-HNSW
Inputs and
1Find to insert into using COMPUTE-JOIN-SET2Insert each vertex into 3for do456FAST-SEARCH-LAYER7SELECT-NEIGHBORS-HEURISTIC8
아래에서 설명하는 절차를 사용하여 집합 계산합니다(1줄). 그런 다음 표준 HNSW 삽입 절차(2줄)를 사용하여 모든 정점을 큰 그래프에 삽입합니다. 삽입하지 않은 각 정점에 대해 삽입한 이웃 정점과 그 이웃 정점을 큰 그래프(4줄과 5줄)에서 찾습니다. 이 집합으로 시드된 FAST-SEARCH-LAYER 절차(6줄)를 사용하여 HNSW 논문 (7줄)에서 SELECT-NEIGHBORS-HEURISTIC 후보를 찾습니다. 사실상 SEARCH-LAYER 을 INSERT 방법(논문의 알고리즘 1)의 후보 집합을 찾는 것으로 대체하는 것이며, 그 외에는 변경 사항이 없습니다. 마지막으로 방금 삽입한 버텍스를 추가합니다(8행).
이 기능이 작동하려면 모든 버텍스에 이웃이 하나 이상 있어야 합니다. 실제로, 우리는 버텍스에 대해 최대 레이어 연결성인 일부 실제 HNSW 그래프에서는 정점 각도가 상당히 분산되어 있는 것을 관찰할 수 있습니다. 아래 그림은 Lucene HNSW 그래프의 최하위 레이어에 대한 일반적인 버텍스 도의 누적 밀도 함수를 보여줍니다.
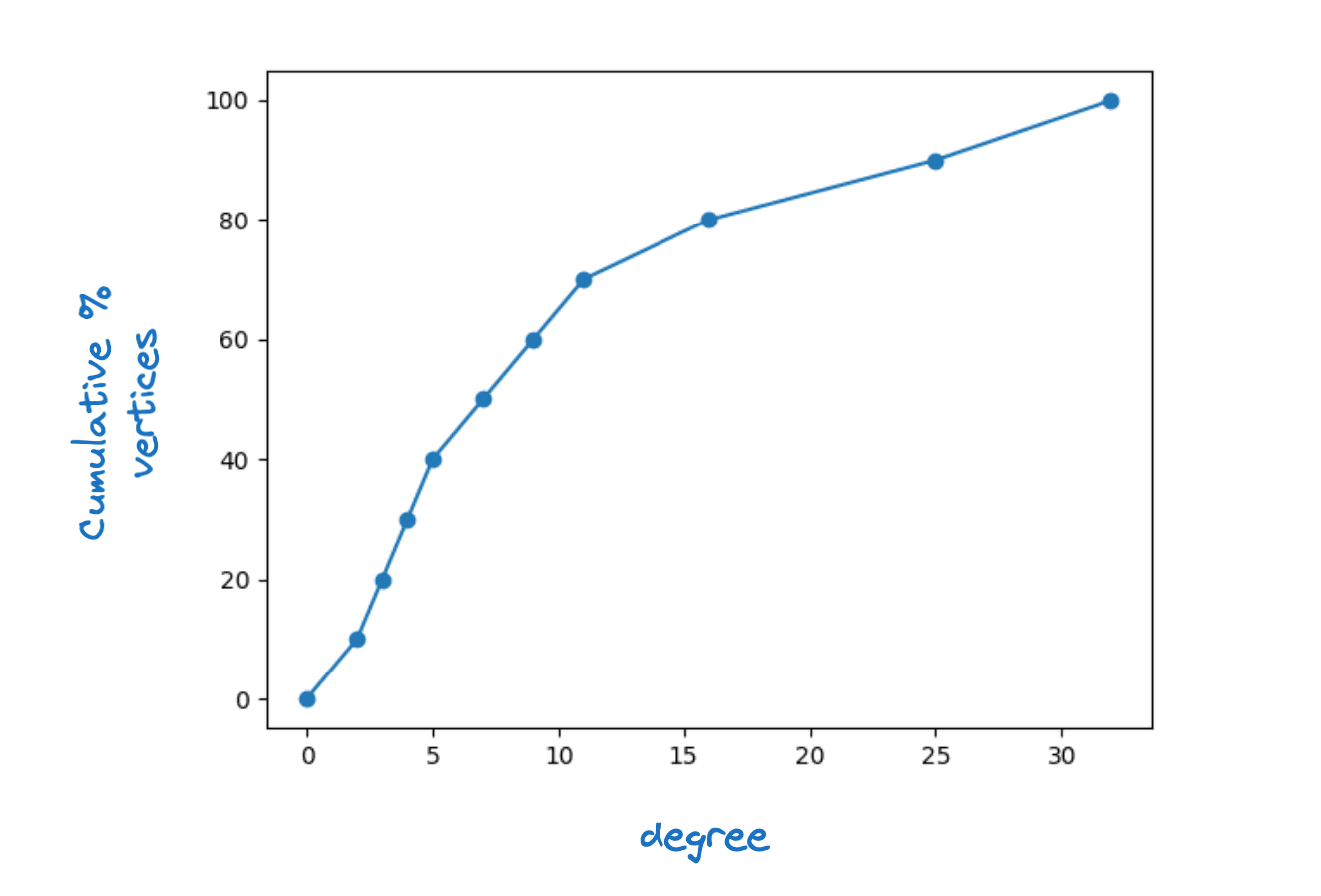
버텍스 차수 분포 예시
고정값을 사용하는 방법과 버텍스 차수의 함수로 만드는 방법을 살펴봤습니다. 두 번째 선택은 그래프 품질에 미치는 영향을 최소화하면서 속도를 크게 향상시킬 수 있으므로 다음과 같이 선택했습니다.
정의상 |는 작은 그래프에서 정점 차수와 같다는 점에 유의하세요. 하한이 2라는 것은 차수가 2보다 작은 모든 정점을 삽입한다는 의미입니다.
간단한 계산 인수를 통해 신중하게 선택하면 직접 삽입하기만 하면 된다는 것을 알 수 있습니다. 구체적으로 그래프의 끝 꼭지점 중 하나를 정확히 삽입하면 그래프의 가장자리에 색을 입힙니다. 최소 이웃을 가지려면 최소 \sum_ k_u{u\in V_s\setminus J} 에지를 채색해야 한다는 것을 알 수 있습니다. 또한 다음을 기대합니다.
여기서 _U\left [N_s(U)|\right] 는 작은 그래프에서 평균 버텍스 차수입니다. 각 정점 u에 대해 최대 의 가장자리를 색칠합니다. 따라서 채색할 에지의 총 개수는 최대 _U\left [|N_s(U)|\right]입니다. 신중하게 선택하면 이 수의 가장자리에 가깝게 색을 칠할 수 있으므로 모든 정점을 포함하려면 다음을 만족해야 합니다.
이는 |J|=\frac{1}{4}(|V_s|-|J|)=\frac{4}{5}\frac {1}{4}|V_s|=\frac{1}{5}|V_s|를 의미합니다.
SEARCH-LAYER 이 런타임을 지배한다면 병합 시간을 최대 단축할 수 있음을 시사합니다. 쓰기 증폭의 대수적 증가를 감안할 때, 이는 매우 큰 인덱스의 경우에도 일반적으로 하나의 그래프를 작성할 때보다 빌드 시간이 두 배밖에 걸리지 않는다는 것을 의미합니다.
이 전략의 위험은 그래프 품질이 손상된다는 점입니다. 처음에는 노옵으로 시도했습니다 FAST-SEARCH-LAYER. 특히 단일 세그먼트로 병합할 때 지연 시간에 따른 리콜이 영향을 받을 정도로 그래프 품질이 저하되는 것으로 나타났습니다. 그런 다음 그래프를 제한적으로 검색하여 다양한 대안을 탐색했습니다. 결국 가장 효과적인 선택은 가장 단순한 것이었습니다. SEARCH-LAYER 을 사용하되 ef_construction. 이 매개변수화를 통해 우수한 품질의 그래프를 얻으면서도 병합 시간을 평균 30% 조금 넘게 줄일 수 있었습니다.
조인 집합 계산
좋은 조인 집합을 찾는 것은 HNSW 그래프 커버링 문제로 공식화할 수 있습니다. 욕심 휴리스틱은 최적의 그래프 커버를 근사화하기 위한 간단하고 효과적인 휴리스틱입니다. 우리가 취하는 접근 방식은 한 번에 하나씩 정점을 골라 이득이 감소하는 순서로 추가하는 방식입니다. 이득은 다음과 같이 정의됩니다:
여기서 는 벡터 개수를 나타내고 은 표시 함수입니다. 이득에는 추가한 버텍스 수의 변화, 즉 이 포함되는데, 이는 덜 커버되는 버텍스를 추가함으로써 목표에 더 가까워지기 때문입니다. 이득 계산은 아래 그림에서 중앙 주황색 버텍스에 대해 설명합니다.
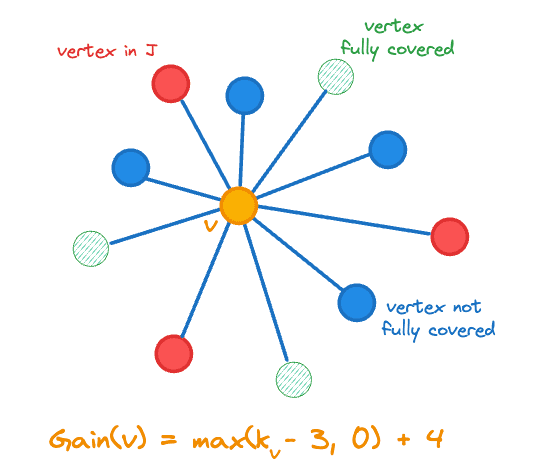
조인 세트 J에 추가할 버텍스 게인
각 버텍스 대해 다음과 같은 상태를 유지합니다:
- 오래되었는지 여부,
- 그 이득 ),
- 인접한 정점의 개수를 로 표시합니다,
- 타이 브레이킹에 사용되는 [0,1] 범위의 난수입니다.
조인 집합을 계산하는 의사 코드는 다음과 같습니다.
COMPUTE-JOIN-SET
Inputs
123for do4567while do
8 maximum gain vertex in 9Remove the state for from 10if is not stale then111213for do14mark as stale if 15mark neighbors of stale if
16
17else
18
19if then
20
21return
먼저 1~5줄에서 상태를 초기화합니다.
메인 루프의 각 반복에서 처음에는 최대 이득 버텍스(8번째 줄)를 추출하여 무작위로 동점을 끊습니다. 변경하기 전에 버텍스의 게인이 오래되었는지 확인해야 합니다. 특히, 버텍스를 추가할 때마다 다른 버텍스의 이득에 영향을 미칩니다:
- 모든 이웃이 추가 이웃을 가지고 있기 때문에 이득이 바뀔 수 있습니다 (14행).
- 이제 이웃이 완전히 커버되면 모든 이웃의 이득이 바뀔 수 있습니다(14~16줄).
게인을 지연 방식으로 다시 계산하므로 버텍스의 게인을 삽입하려는 경우에만 다시 계산합니다(18~20행). 이득은 항상 감소하기 때문에 삽입해야 하는 버텍스를 놓칠 수 없습니다.
종료 시점을 결정하기 위해 추가한 버텍스의 총 이득을 추적하기만 하면 됩니다. 또한, Gain_{tot}< Gain_ {exit}적어도 하나의 버텍스는 0이 아닌 이득을 가지므로 항상 진전이 있습니다.
결과
지원되는 세 가지 거리 메트릭(유클리드, 코사인, 내적 곱)을 모두 포함하는 네 가지 데이터 세트에 대해 실험을 진행했습니다:
- 쿼라-E5-small: 522931개 문서, 384개 차원, 코사인 유사도를 사용합니다,
- 코히어-위키백과-v2: 1백만 개의 문서, 768개의 차원, 코사인 유사도를 사용합니다,
- 요점 1백만 문서, 960개 차원, 유클리드 거리 사용, 그리고
- 코히어-위키백과-v3: 1M 문서, 1024 크기, 최대 내부 제품 사용.
각 데이터 세트에 대해 두 가지 양자화 수준을 평가합니다:
- int8 - 차원당 1바이트 정수를 사용하고
- BBQ - 차원당 단일 비트를 사용합니다.
마지막으로, 각 실험에서 두 가지 검색 깊이에서 검색 품질을 평가하고 인덱스를 구축한 후와 단일 세그먼트로 강제 병합한 후를 조사했습니다.
요약하면, 모든 경우에서 그래프 품질을 유지하면서 인덱싱 및 병합 속도를 일관되게 크게 향상시켜 검색 성능을 향상시켰습니다.
실험 1: int8 정량화
베이스라인에서 제안된 변경 사항인 후보까지의 평균 속도 향상은 다음과 같습니다:
색인 시간 속도 향상: 1.
강제 병합 속도 향상: 1.
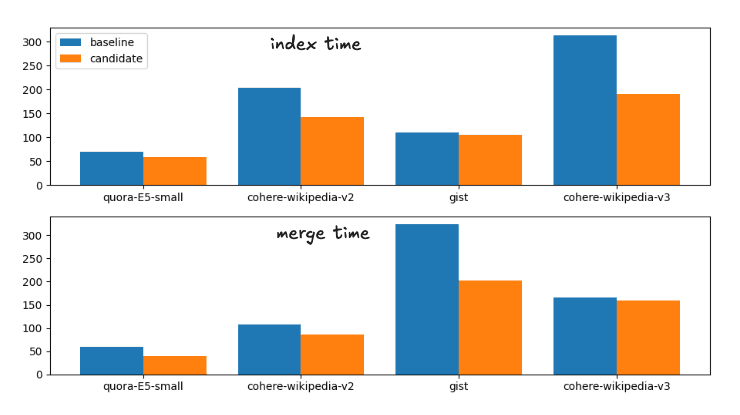
이는 다음과 같은 실행 시간 분석에 해당합니다.
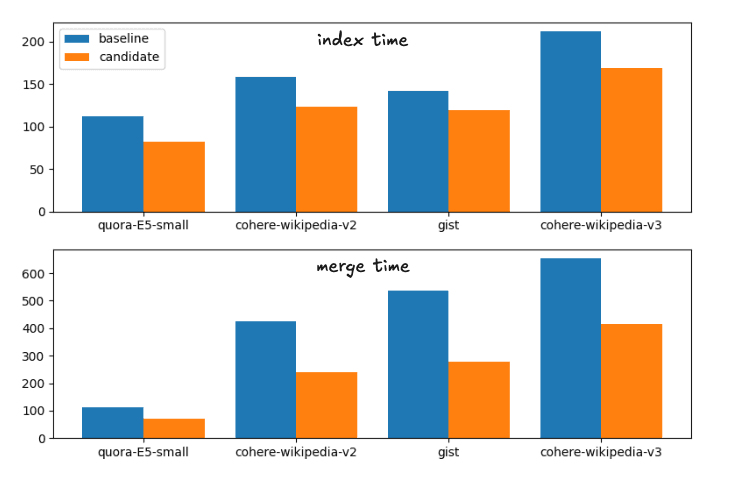
기준 및 후보 병합 전략에 대한 인덱싱 및 병합 시간
정확성을 위해 정확한 시간은 다음과 같습니다.
| 색인 | 병합 | |||
|---|---|---|---|---|
| 데이터 세트 | 기준선 | 후보 | 구축 | 후보 |
| 쿼라-E5-small | 112.41s | 81.55s | 113.81s | 70.87s |
| 위키-코히어-v2 | 158.1s | 122.95s | 425.20s | 239.28s |
| 요점 | 141.82s | 119.26s | 536.07s | 279.05s |
| 위키-코히어-v3 | 211.86s | 168.22s | 654.97s | 414.12s |
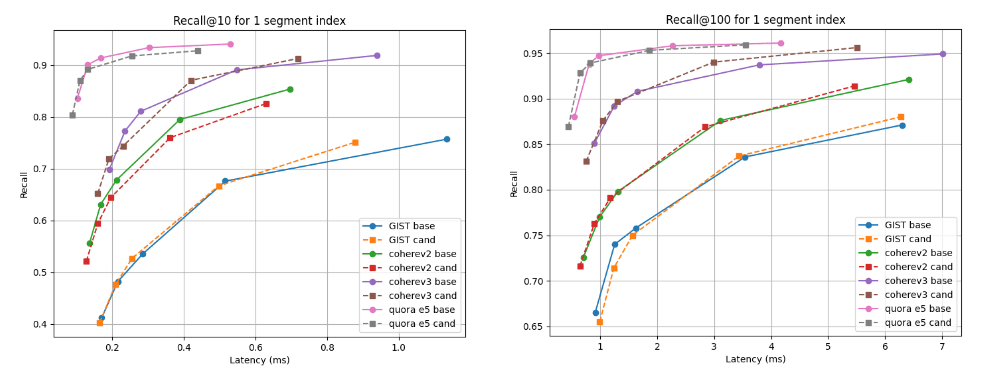
아래에는 여러 세그먼트가 있는 인덱스(모든 벡터를 인덱싱한 후 기본 병합 전략의 최종 결과)와 단일 세그먼트로 강제 병합한 후의 두 가지 검색 깊이인 recall@10과 recall@100에서 후보(점선)와 기준선을 비교한 리콜 대 지연 시간 그래프가 나와 있습니다. 곡선이 더 높고 왼쪽으로 갈수록 더 좋은데, 이는 더 낮은 지연 시간에서 더 높은 회상률을 의미합니다.
보시다시피, 여러 세그먼트 인덱스의 경우 Cohere v3 데이터 세트의 후보가 더 우수하고 다른 모든 데이터 세트의 경우 약간 떨어지지만 거의 비슷합니다. 단일 세그먼트로 병합한 후 리콜 곡선은 모든 경우에 대해 거의 동일합니다.
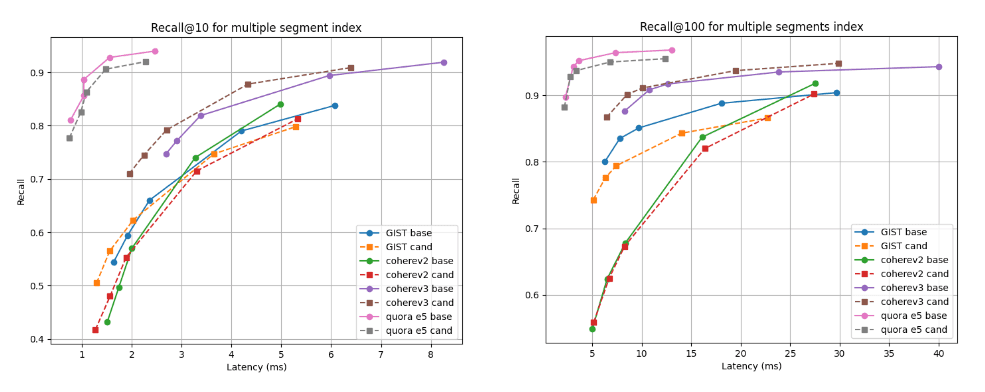
인덱스 구축 후 지연 시간 대비 @10 및 @100 리콜하기
단일 세그먼트로 병합 후 지연 시간 대비 @10 및 @100 리콜하기
실험 2: BBQ 정량화
기준선에서 후보까지의 평균 속도 향상은 다음과 같습니다:
색인 시간 속도 향상: 1.
강제 병합 속도 향상: 1.
이는 다음과 같은 실행 시간 분석에 해당합니다.
기준 및 후보 병합 전략에 대한 인덱싱 및 병합 시간
정확성을 위해 정확한 시간은 다음과 같습니다.
| 색인 | 병합 | |||
|---|---|---|---|---|
| 데이터 세트 | 기준선 | 후보 | 구축 | 후보 |
| 쿼라-E5-small | 70.71s | 58.25s | 59.38s | 40.15s |
| 위키-코히어-v2 | 203.08s | 142.27s | 107.27s | 85.68s |
| 요점 | 110.35s | 105.52s | 323.66s | 202.2s |
| 위키-코히어-v3 | 313.43s | 190.63s | 165.98s | 159.95s |
여러 세그먼트 인덱스의 경우, 기준선이 약간 더 나은 코히어 v2를 제외한 거의 모든 데이터 세트에서 후보가 더 우수합니다. 단일 세그먼트 인덱스의 경우 리콜 곡선은 모든 경우에 대해 거의 동일합니다.
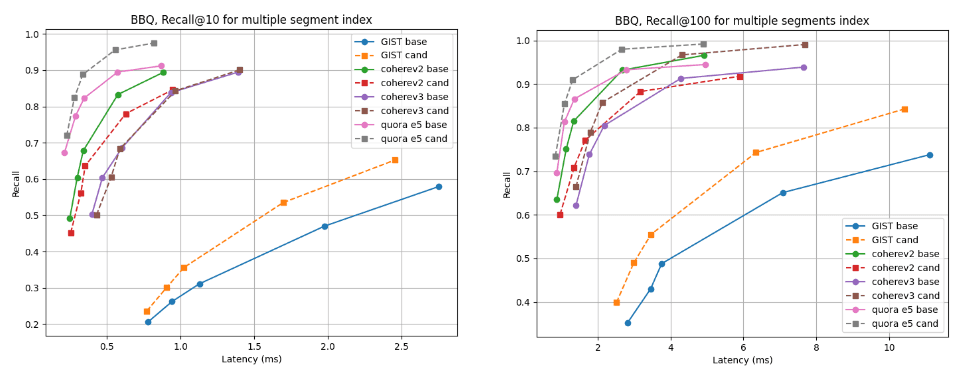
인덱스 구축 후 지연 시간 대비 @10 및 @100 리콜하기
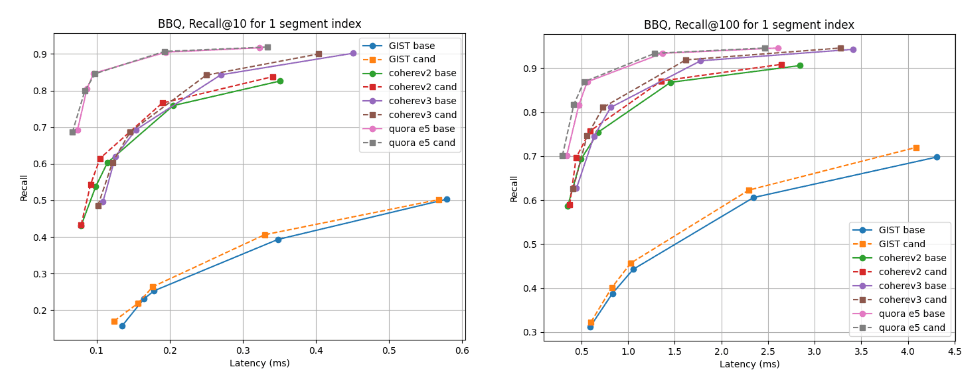
단일 세그먼트로 병합된 지연 시간 대비 @10 및 @100을 기억해 보세요.
결론
이 블로그에서 설명한 알고리즘은 곧 출시될 Lucene 10.2와 이를 기반으로 하는 Elasticsearch 릴리즈에서 사용할 수 있습니다. 사용자는 이 새 버전에서 병합 성능이 향상되고 인덱스 빌드 시간이 단축되는 이점을 누릴 수 있습니다. 이 변경은 벡터 및 하이브리드 검색을 위한 빠르고 효율적인 Lucene과 Elasticsearch를 만들기 위한 지속적인 노력의 일환입니다.




