从向量搜索到强大的 REST API,Elasticsearch 为开发人员提供了最全面的搜索工具包。探索 GitHub 上的示例笔记本,尝试新事物。您也可以立即开始免费试用或在本地运行 Elasticsearch。
过去,我们讨论过搜索多个HNSW 图表所面临的一些挑战,以及我们是如何缓解这些挑战的。当时,我们提到了我们计划进行的一些进一步改进。这篇文章就是这项工作的结晶。
你可能会问,为什么要使用多图表呢?这是 Lucene 架构选择的副作用:不可变的段。与大多数建筑选择一样,有利也有弊。例如,我们最近对无服务器 Elasticsearch 进行了 GA。在这种情况下,我们从不可变分段中获得了非常显著的优势,包括高效的索引复制以及将索引和查询计算解耦并独立自动扩展的能力。对于矢量量化,分段合并让我们有机会更新参数,使其适应数据特征。按照这种思路,我们认为有机会测量数据特征和重新审视索引选择还有其他好处。
在这篇文章中,我们将讨论我们为大幅降低构建多个 HNSW 图形的开销,尤其是降低合并图形的成本所做的工作。
背景
为了保持可管理的分段数量,Lucene 会定期检查是否应该合并分段。这相当于检查当前分段数是否超过目标分段数,目标分段数由基本分段大小和合并策略决定。如果超过该计数,Lucene 会合并片段组,同时违反约束条件。这一过程在其他地方有详细描述。
Lucene 选择合并大小相似的数据段,因为这样可以实现写入放大的对数增长。就向量索引而言,写入放大是指向量插入图形的次数。Lucene 会尝试以大约 10 个为一组合并数据段。因此,向量插入图的次数大约为1+\frac{9}{10} \log_ {10}\left (\frac{n}{n_0} \right ) 次,其中是索引向量数,n 是预期的基本段向量数。由于写入量呈对数增长,即使是庞大的指数,写入放大率也只有个位数。不过,合并图形所花费的总时间与写入放大率成线性比例。
在合并 HNSW 图形时,我们已经进行了小幅优化:保留最大分段的图形,并将其他分段的向量插入其中。这就是上述 9/10 因素的原因。下面,我们将展示如何通过使用我们正在合并的所有图表中的信息来大幅提高性能。
HNSW 图表合并
此前,我们保留了最大的图形,并从其他图形中插入矢量,但忽略了包含这些矢量的图形。我们在下文中利用的关键见解是,我们丢弃的每个 HNSW 图形都包含了有关其所含向量的重要邻近性信息。我们希望利用这些信息来加快插入至少部分载体的速度。
我们重点讨论将较小的图插入较大的图 _l=(V _l, E _l)的问题,因为这是一个原子操作,我们可以用它来构建任何合并策略。
策略是找到的一个顶点子集,将其插入大图中。然后,我们利用这些顶点在小图中的连通性,加速插入剩余的顶点。在下文中,我们用和分别表示小图和大图中顶点的邻居。具体流程如下
MERGE-HNSW
Inputs and
1Find to insert into using COMPUTE-JOIN-SET2Insert each vertex into 3for do456FAST-SEARCH-LAYER7SELECT-NEIGHBORS-HEURISTIC8
我们使用下面讨论的程序来计算集合(第 1 行)。然后,我们使用标准的 HNSW 插入程序将中的每个顶点插入大图中(第 2 行)。对于我们尚未插入的每个顶点,我们都要找到已插入的邻接顶点及其在大图中的邻接顶点(第 4 行和第 5 行)。我们使用FAST-SEARCH-LAYER 程序(第 6 行)作为种子程序,从 HNSW论文(第 7 行)中找到SELECT-NEIGHBORS-HEURISTIC 的候选者。实际上,我们在INSERT 方法(论文中的算法 1)中替换了SEARCH-LAYER 来查找候选集,其他方面没有变化。最后,我们将刚刚插入的顶点添加到(第 8 行)。
很明显,要做到这一点,中的每个顶点都必须在至少有一个邻居。事实上,我们要求对于中的每个顶点,|J\capfor some M,即最大层连接性。我们观察到,在真实的 HNSW 图中,顶点度的分布相当广泛。下图显示了 Lucene HNSW 图表底层顶点度的典型累积密度函数。
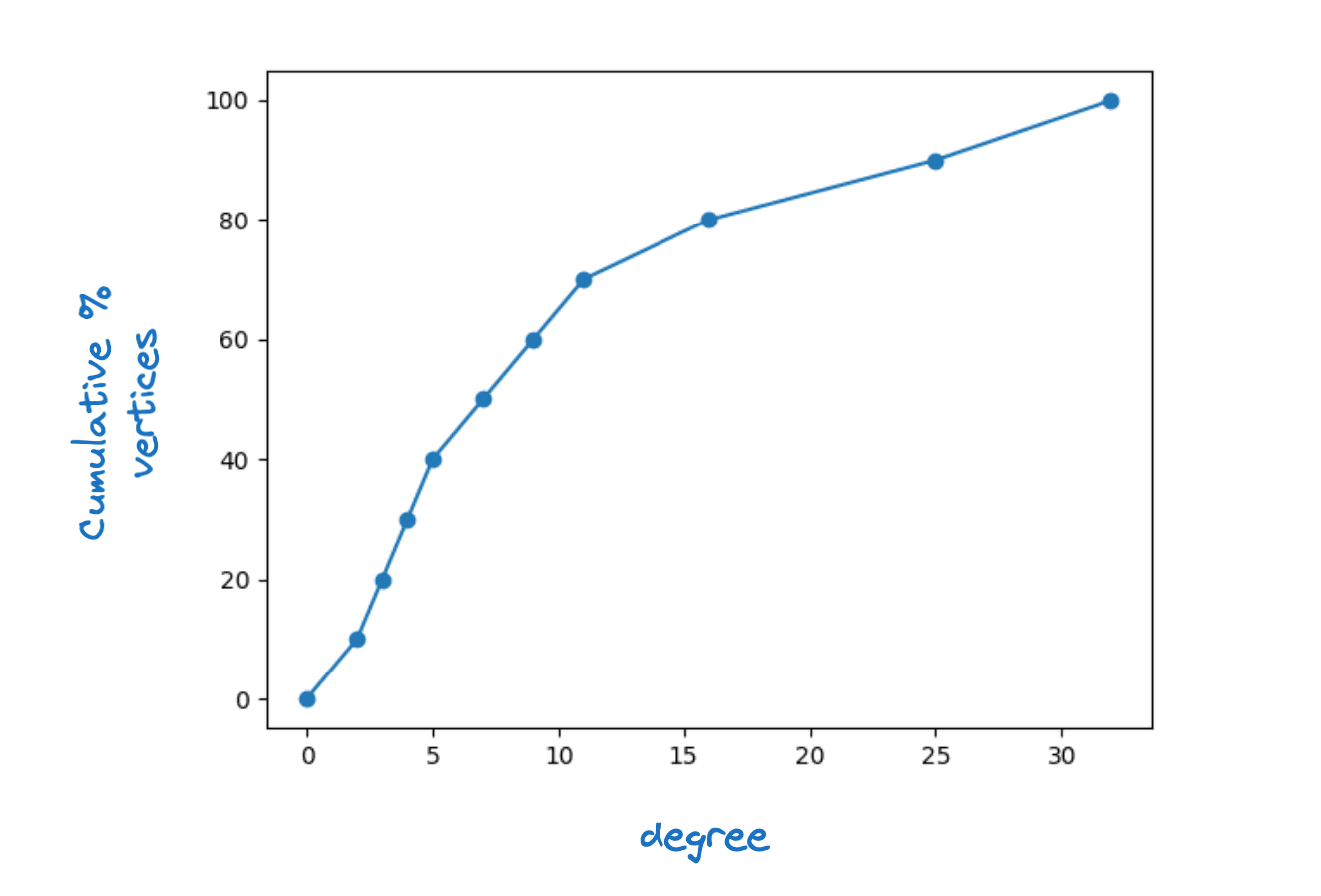
顶点度分布示例
我们探讨了的固定值以及使其成为顶点度函数的方法。第二种选择会带来更快的速度,而对图形质量的影响却很小,因此采用了以下方案
请注意,根据定义,|N_s| 等于小图中顶点的度数。下限为 2 意味着我们将插入每个度数小于 2 的顶点。
一个简单的计数论证表明,如果我们仔细选择 ,我们只需要在 中直接插入大约具体来说,如果我们将一条图边的一个末端顶点恰好插入到,我们就会给这条图边着色。那么我们知道,对于 中 至少有 个 邻居,我们至少需要给 条边着色。此外,我们预计
这里,_U(left[N_s(U)|\right])是小图中的平均顶点度。对于每个顶点u\我们最多为 |N_s条边着色。因此,我们期望着色的边的总数最多为 |J|\_U\left[|N_s(U)|\right].我们希望通过仔细选择,使着色的边数接近这一数字,因此,为了覆盖所有顶点,J| 需要满足以下条件
这意味着|J|=\frac{1}{4} (|V_s|-|J|)=\frac{4}{5} \frac {1}{4}|V_s|=\frac{1}{5} |V_s|。
如果SEARCH-LAYER 的运行时间占主导地位,这表明我们可以将合并时间最多提高。考虑到写入放大率的对数增长,这意味着即使对于非常大的索引,我们的构建时间通常也只比构建一个图形多一倍。
这种策略的风险在于会破坏图形质量。我们最初尝试使用无操作程序FAST-SEARCH-LAYER 。我们发现这降低了图表质量,以至于影响了作为延迟函数的召回率,尤其是在合并到单个片段时。然后,我们通过对图形的有限搜索,探索了各种替代方案。最终,最有效的选择是最简单的。使用SEARCH-LAYER ,但ef_construction 要低。通过这种参数设置,我们能够获得质量极佳的图形,同时还能将合并时间平均缩短 30% 多一点。
计算连接集
寻找一个好的连接集可以表述为一个 HNSW 图覆盖问题。贪婪启发式是一种简单有效的近似最优图覆盖的启发式。我们采用的方法是按增益递减的顺序逐个选取顶点添加到。增益定义如下
这里,表示向量在中的邻域数,是指示函数。增益包括我们添加到的顶点计数的变化,即 \max,因为我们添加了一个覆盖范围较小的顶点,从而更接近我们的目标。下图展示了中心橙色顶点的增益计算。
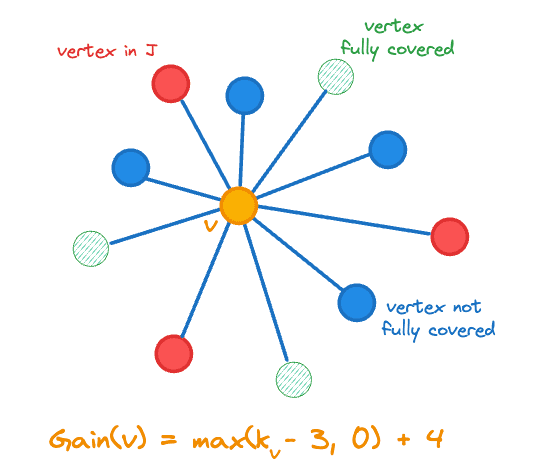
加入连接集 J 的顶点增益
我们为每个顶点 维护以下状态
- 是否陈旧、
- 其增益
- 中相邻顶点的计数,用 表示、
- 范围为 [0,1] 的随机数,用于打破平局。
计算连接集的伪代码如下。
COMPUTE-JOIN-SET
Inputs
123for do4567while do
8 maximum gain vertex in 9Remove the state for from 10if is not stale then111213for do14mark as stale if 15mark neighbors of stale if
16
17else
18
19if then
20
21return
我们首先在第 1-5 行中初始化状态。
在主循环的每次迭代中,我们首先提取最大增益顶点(第 8 行),然后随机打破平局。在进行任何更改之前,我们需要检查顶点的增益是否过时。特别是,每次我们将一个顶点添加到,都会影响其他顶点的增益:
- 由于它的所有邻居在中都多了一个邻居,因此它们的收益会发生变化(第 14 行)
- 如果它的任何一个邻居现在被完全覆盖,其所有邻居的收益都会发生变化(第 14-16 行)
我们以一种懒散的方式重新计算增益,因此只有当我们想要将某个顶点插入,才会重新计算该顶点的增益(第 18-20 行)。由于增益只会减少,我们永远不会错过应该插入的顶点。
请注意,我们只需跟踪我们添加到的顶点的总增益,就能确定何时退出。此外,当Gain_{tot}< Gain_ {exit} 时,至少有一个顶点的增益不为零,因此我们总能取得进展。
实施结果
我们在四个数据集上进行了实验,这四个数据集涵盖了我们支持的三种距离度量(欧氏、余弦和内积):
- quora-E5-small:522931 个文档,384 个维度,使用余弦相似性、
- cohere-wikipedia-v2:1M 文档,768 维度,使用余弦相似性、
- gist:100 万个文档、960 个维度并使用欧氏距离,以及
- cohere-wikipedia-v3:100 万文档,1024 维度,使用最大内积。
对于每个数据集,我们都会评估两种量化水平:
- int8 - 每个维度使用一个 1 字节的整数,而
- BBQ - 每个维度使用一个比特。
最后,在每个实验中,我们在两个检索深度对搜索质量进行了评估,并在建立索引后和强制合并为单一片段后对搜索质量进行了检查。
总之,我们在索引和合并方面实现了持续的大幅提速,同时保持了图的质量,因此在所有情况下都能保持搜索性能。
实验 1:int8 量化
从基线到候选方案(建议的修改)的平均提速为
索引时间加速:1. 次
强制合并加速:1. 次
运行时间细分如下
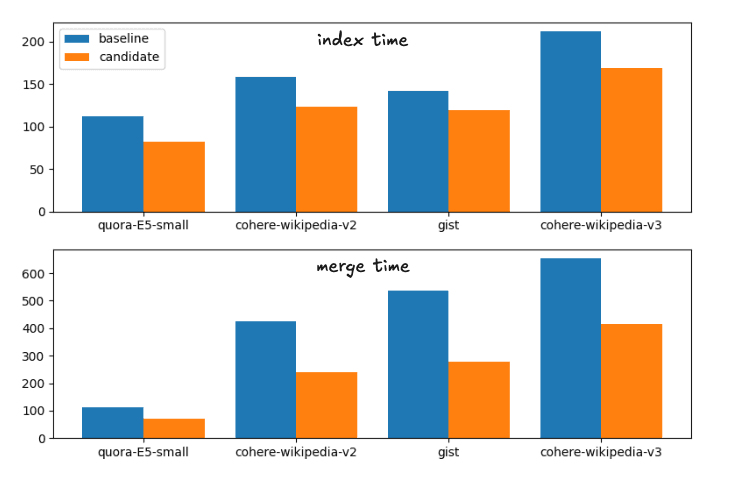
基线和候选合并策略的索引和合并时间
为完整起见,确切时间为
| 索引 | 合并 | |||
|---|---|---|---|---|
| 数据集 | 底线 | 候选人 | 构建 | 候选人 |
| quora-E5-small | 112.41s | 81.55s | 113.81s | 70.87s |
| wiki-cohere-v2 | 158.1s | 122.95s | 425.20s | 239.28s |
| 要领 | 141.82s | 119.26s | 536.07s | 279.05s |
| wiki-cohere-v3 | 211.86s | 168.22s | 654.97s | 414.12s |
下面我们展示了候选方案(虚线)与基线在两种检索深度下的召回率与延迟对比图:多段索引的召回率@10 和召回率@100(我们的默认合并策略在索引所有矢量后的最终结果),以及强制合并为单段后的召回率与延迟对比图。曲线越高、越靠左越好,这意味着在较低的延迟条件下有更高的记忆率。
正如您所看到的,对于 Cohere v3 数据集来说,候选者的多分段指数更好,而对于所有其他数据集来说,候选者的多分段指数稍差,但几乎不相上下。合并为单一网段后,所有情况下的召回曲线几乎相同。
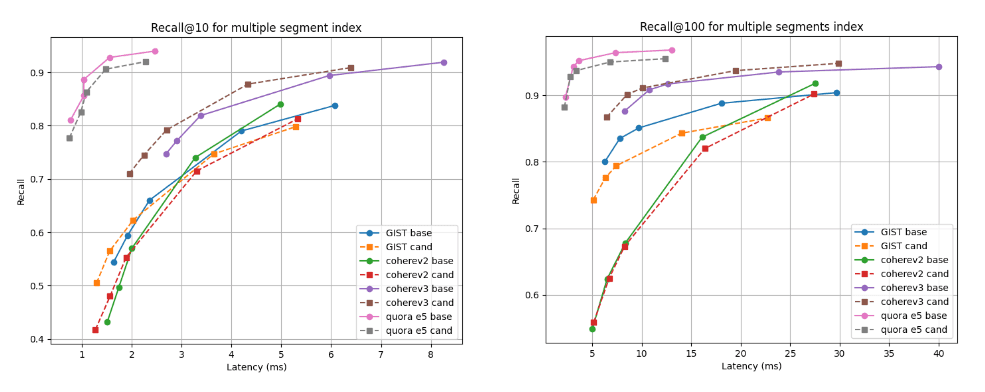
建立索引后的 10 倍和 100 倍召回率与延迟时间对比
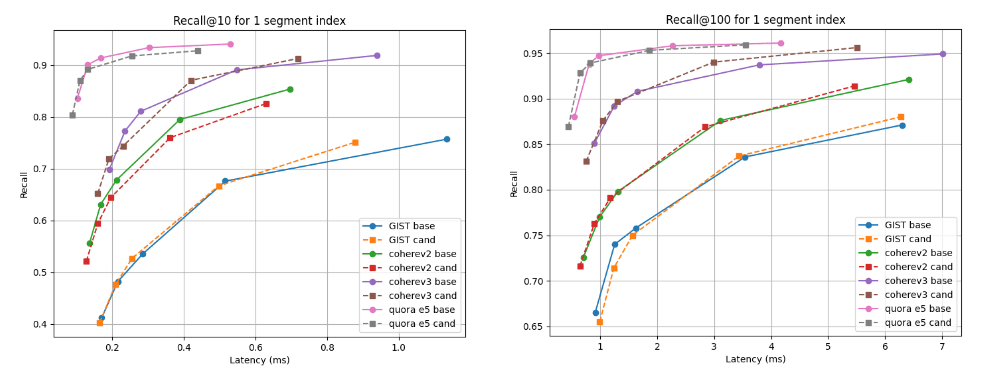
合并为单一网段后,10 和 100 的召回率与延迟对比
实验 2:烧烤量化
从基准线到候选方案的平均加速度为
索引时间加速:1. 次
强制合并加速:1. 次
运行时间细分如下
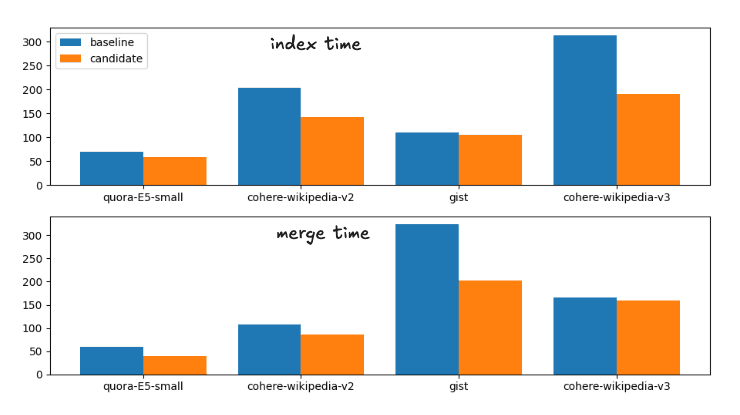
基线和候选合并策略的索引和合并时间
为完整起见,确切时间为
| 索引 | 合并 | |||
|---|---|---|---|---|
| 数据集 | 底线 | 候选人 | 构建 | 候选人 |
| quora-E5-small | 70.71s | 58.25s | 59.38s | 40.15s |
| wiki-cohere-v2 | 203.08s | 142.27s | 107.27s | 85.68s |
| 要领 | 110.35s | 105.52s | 323.66s | 202.2s |
| wiki-cohere-v3 | 313.43s | 190.63s | 165.98s | 159.95s |
对于多分段索引,候选者在几乎所有数据集上都更胜一筹,但 cohere v2 除外,基线略胜一筹。就单段指数而言,所有情况下的召回曲线几乎相同。
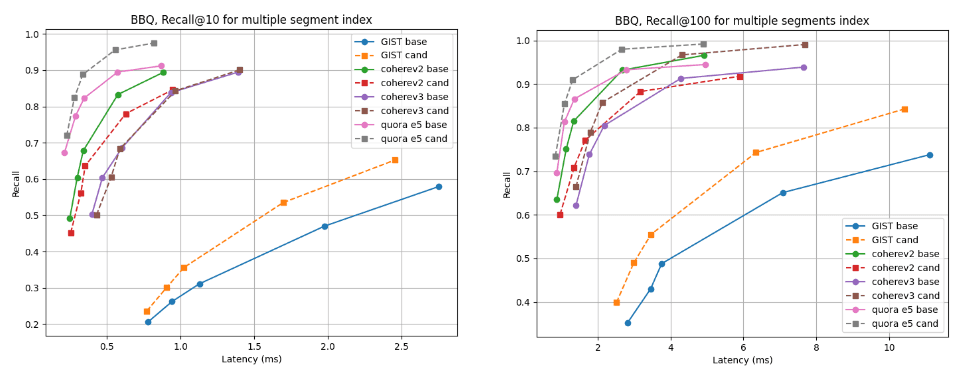
建立索引后的 10 倍和 100 倍召回率与延迟时间对比
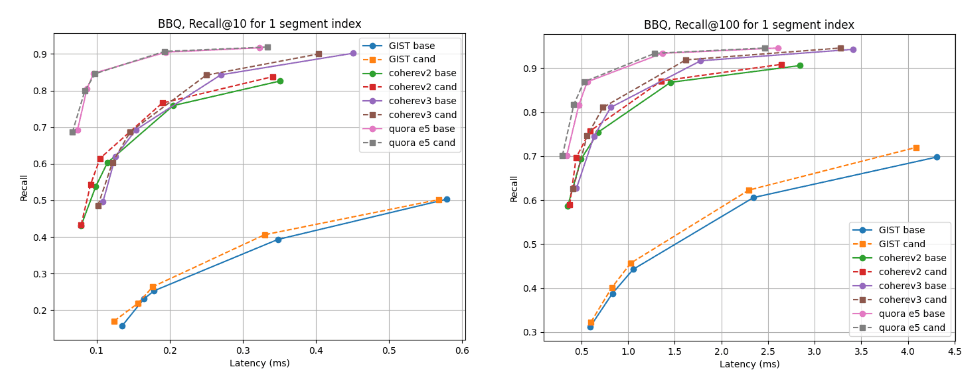
恢复 @10 和 @100 与合并为单一分段后的延迟对比
结论
本博客中讨论的算法将在即将发布的 Lucene 10.2 以及基于该算法的 Elasticsearch 版本中提供。用户将能利用这些新版本中改进的合并性能和缩短的索引构建时间。这一变更是我们为使 Lucene 和 Elasticsearch 在矢量和混合搜索方面快速高效而不断努力的一部分。




