Percentiles Aggregation
editPercentiles Aggregation
editA multi-value metrics aggregation that calculates one or more percentiles
over numeric values extracted from the aggregated documents. These values can be
generated by a provided script or extracted from specific numeric or
histogram fields in the documents.
Percentiles show the point at which a certain percentage of observed values occur. For example, the 95th percentile is the value which is greater than 95% of the observed values.
Percentiles are often used to find outliers. In normal distributions, the 0.13th and 99.87th percentiles represents three standard deviations from the mean. Any data which falls outside three standard deviations is often considered an anomaly.
When a range of percentiles are retrieved, they can be used to estimate the data distribution and determine if the data is skewed, bimodal, etc.
Assume your data consists of website load times. The average and median load times are not overly useful to an administrator. The max may be interesting, but it can be easily skewed by a single slow response.
Let’s look at a range of percentiles representing load time:
GET latency/_search
{
"size": 0,
"aggs" : {
"load_time_outlier" : {
"percentiles" : {
"field" : "load_time"
}
}
}
}
By default, the percentile metric will generate a range of
percentiles: [ 1, 5, 25, 50, 75, 95, 99 ]. The response will look like this:
{
...
"aggregations": {
"load_time_outlier": {
"values" : {
"1.0": 5.0,
"5.0": 25.0,
"25.0": 165.0,
"50.0": 445.0,
"75.0": 725.0,
"95.0": 945.0,
"99.0": 985.0
}
}
}
}
As you can see, the aggregation will return a calculated value for each percentile in the default range. If we assume response times are in milliseconds, it is immediately obvious that the webpage normally loads in 10-725ms, but occasionally spikes to 945-985ms.
Often, administrators are only interested in outliers — the extreme percentiles. We can specify just the percents we are interested in (requested percentiles must be a value between 0-100 inclusive):
GET latency/_search
{
"size": 0,
"aggs" : {
"load_time_outlier" : {
"percentiles" : {
"field" : "load_time",
"percents" : [95, 99, 99.9]
}
}
}
}
Keyed Response
editBy default the keyed flag is set to true which associates a unique string key with each bucket and returns the ranges as a hash rather than an array. Setting the keyed flag to false will disable this behavior:
GET latency/_search
{
"size": 0,
"aggs": {
"load_time_outlier": {
"percentiles": {
"field": "load_time",
"keyed": false
}
}
}
}
Response:
{
...
"aggregations": {
"load_time_outlier": {
"values": [
{
"key": 1.0,
"value": 5.0
},
{
"key": 5.0,
"value": 25.0
},
{
"key": 25.0,
"value": 165.0
},
{
"key": 50.0,
"value": 445.0
},
{
"key": 75.0,
"value": 725.0
},
{
"key": 95.0,
"value": 945.0
},
{
"key": 99.0,
"value": 985.0
}
]
}
}
}
Script
editThe percentile metric supports scripting. For example, if our load times are in milliseconds but we want percentiles calculated in seconds, we could use a script to convert them on-the-fly:
GET latency/_search
{
"size": 0,
"aggs" : {
"load_time_outlier" : {
"percentiles" : {
"script" : {
"lang": "painless",
"source": "doc['load_time'].value / params.timeUnit",
"params" : {
"timeUnit" : 1000
}
}
}
}
}
}
|
The |
|
|
Scripting supports parameterized input just like any other script |
This will interpret the script parameter as an inline script with the painless script language and no script parameters. To use a stored script use the following syntax:
GET latency/_search
{
"size": 0,
"aggs" : {
"load_time_outlier" : {
"percentiles" : {
"script" : {
"id": "my_script",
"params": {
"field": "load_time"
}
}
}
}
}
}
Percentiles are (usually) approximate
editThere are many different algorithms to calculate percentiles. The naive
implementation simply stores all the values in a sorted array. To find the 50th
percentile, you simply find the value that is at my_array[count(my_array) * 0.5].
Clearly, the naive implementation does not scale — the sorted array grows linearly with the number of values in your dataset. To calculate percentiles across potentially billions of values in an Elasticsearch cluster, approximate percentiles are calculated.
The algorithm used by the percentile metric is called TDigest (introduced by
Ted Dunning in
Computing Accurate Quantiles using T-Digests).
When using this metric, there are a few guidelines to keep in mind:
-
Accuracy is proportional to
q(1-q). This means that extreme percentiles (e.g. 99%) are more accurate than less extreme percentiles, such as the median - For small sets of values, percentiles are highly accurate (and potentially 100% accurate if the data is small enough).
- As the quantity of values in a bucket grows, the algorithm begins to approximate the percentiles. It is effectively trading accuracy for memory savings. The exact level of inaccuracy is difficult to generalize, since it depends on your data distribution and volume of data being aggregated
The following chart shows the relative error on a uniform distribution depending on the number of collected values and the requested percentile:
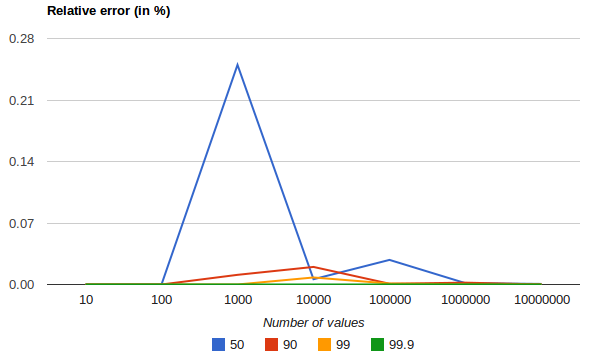
It shows how precision is better for extreme percentiles. The reason why error diminishes for large number of values is that the law of large numbers makes the distribution of values more and more uniform and the t-digest tree can do a better job at summarizing it. It would not be the case on more skewed distributions.
Percentile aggregations are also non-deterministic. This means you can get slightly different results using the same data.
Compression
editApproximate algorithms must balance memory utilization with estimation accuracy.
This balance can be controlled using a compression parameter:
GET latency/_search
{
"size": 0,
"aggs" : {
"load_time_outlier" : {
"percentiles" : {
"field" : "load_time",
"tdigest": {
"compression" : 200
}
}
}
}
}
The TDigest algorithm uses a number of "nodes" to approximate percentiles — the
more nodes available, the higher the accuracy (and large memory footprint) proportional
to the volume of data. The compression parameter limits the maximum number of
nodes to 20 * compression.
Therefore, by increasing the compression value, you can increase the accuracy of
your percentiles at the cost of more memory. Larger compression values also
make the algorithm slower since the underlying tree data structure grows in size,
resulting in more expensive operations. The default compression value is
100.
A "node" uses roughly 32 bytes of memory, so under worst-case scenarios (large amount of data which arrives sorted and in-order) the default settings will produce a TDigest roughly 64KB in size. In practice data tends to be more random and the TDigest will use less memory.
HDR Histogram
editThis setting exposes the internal implementation of HDR Histogram and the syntax may change in the future.
HDR Histogram (High Dynamic Range Histogram) is an alternative implementation that can be useful when calculating percentiles for latency measurements as it can be faster than the t-digest implementation with the trade-off of a larger memory footprint. This implementation maintains a fixed worse-case percentage error (specified as a number of significant digits). This means that if data is recorded with values from 1 microsecond up to 1 hour (3,600,000,000 microseconds) in a histogram set to 3 significant digits, it will maintain a value resolution of 1 microsecond for values up to 1 millisecond and 3.6 seconds (or better) for the maximum tracked value (1 hour).
The HDR Histogram can be used by specifying the method parameter in the request:
GET latency/_search
{
"size": 0,
"aggs" : {
"load_time_outlier" : {
"percentiles" : {
"field" : "load_time",
"percents" : [95, 99, 99.9],
"hdr": {
"number_of_significant_value_digits" : 3
}
}
}
}
}
|
|
|
|
|
The HDRHistogram only supports positive values and will error if it is passed a negative value. It is also not a good idea to use the HDRHistogram if the range of values is unknown as this could lead to high memory usage.
Missing value
editThe missing parameter defines how documents that are missing a value should be treated.
By default they will be ignored but it is also possible to treat them as if they
had a value.